瘋癲爺 拙痴无の戯言・放言・歯軋り
円の性質について15の提議が書かれたArchimedes(アルキメデス)の『補助定理集』(Book of Lemmas) は、アラブ語で書かれた写しが知られている。ここには、arbelos(アルベロス)の研究があるという。
 まず、線分ABを直径とする半円γを描き、次に線分AB上に点Cをとり、線分ACおよび線分BCを直径とする半円α、βを同じ側に描く。これらの3つの半円α、β、γで囲まれる図形がarbelos(アルベロス)といわれている図形である。すなわち、1つの半円γのなかに、2つの半円α、βをちょうど接するように描かれたもので、その3つの半円の円弧で囲まれた図形をarbelos(アルベロス)と呼ばれている。その形が古代ギリシャで使われていたらしい「靴屋のナイフ」(ギリシャ語でアルベロス)に似ていたことから、Archimedes(アルキメデス)が名付けたものだといわれている。
まず、線分ABを直径とする半円γを描き、次に線分AB上に点Cをとり、線分ACおよび線分BCを直径とする半円α、βを同じ側に描く。これらの3つの半円α、β、γで囲まれる図形がarbelos(アルベロス)といわれている図形である。すなわち、1つの半円γのなかに、2つの半円α、βをちょうど接するように描かれたもので、その3つの半円の円弧で囲まれた図形をarbelos(アルベロス)と呼ばれている。その形が古代ギリシャで使われていたらしい「靴屋のナイフ」(ギリシャ語でアルベロス)に似ていたことから、Archimedes(アルキメデス)が名付けたものだといわれている。
このアルベロス図形は、さまざまに面白い性質を持っていて、そのために、昔から多くの人が関心を寄せ、いまなお世界各地で研究され、研究は進化しつづけているという。Arbelos(アルベロス)というのは、古代ギリシアのArchimedes(アルキメデス)の頃から多くの数学者たちを魅了し、日本の和算家たちにも取上げられ、なお現在もホットな研究が続けられている平面図形であるという。
 左図に示すように、アルベロスの面積は容易に求められ、この値は、驚くべきことに、図の垂線CDを直径とする円の面積に等しくなるのである。(左図参照)
左図に示すように、アルベロスの面積は容易に求められ、この値は、驚くべきことに、図の垂線CDを直径とする円の面積に等しくなるのである。(左図参照)
さらに、左図のように半円A、Bの共通接線の接点を結ぶ線分EFと線分CDを対角線にもつ四角形CFDEを作ると、四角形CFDEは長方形になるという美しい性質がある。(左図の証明参照)
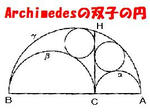 このアルベロス図形は,さまざまに面白い性質をもつが、なかでも,アルキメデスの双子の円と呼ばれる問題が有名である。左図で半円内の大きい方の円の半径をa、小さい方の円の半径をb とし、円内の2つの半円の交点を通る半円に垂直な線CHを引くと、その直線と内円と外円に接している円の半径はともに、ab/(a+b)という式で表されることも知られている。
このアルベロス図形は,さまざまに面白い性質をもつが、なかでも,アルキメデスの双子の円と呼ばれる問題が有名である。左図で半円内の大きい方の円の半径をa、小さい方の円の半径をb とし、円内の2つの半円の交点を通る半円に垂直な線CHを引くと、その直線と内円と外円に接している円の半径はともに、ab/(a+b)という式で表されることも知られている。
このアルベロス図形は、さまざまに面白い性質を持っていて、そのために、昔から多くの人が関心を寄せ、いまなお世界各地で研究され、研究は進化しつづけているという。Arbelos(アルベロス)というのは、古代ギリシアのArchimedes(アルキメデス)の頃から多くの数学者たちを魅了し、日本の和算家たちにも取上げられ、なお現在もホットな研究が続けられている平面図形であるという。
さらに、左図のように半円A、Bの共通接線の接点を結ぶ線分EFと線分CDを対角線にもつ四角形CFDEを作ると、四角形CFDEは長方形になるという美しい性質がある。(左図の証明参照)
PR
この記事にコメントする
プロフィール
ハンドルネーム:
目高 拙痴无
年齢:
93
誕生日:
1932/02/04
自己紹介:
くたばりかけの糞爺々です。よろしく。メールも頼むね。
sechin@nethome.ne.jp です。
sechin@nethome.ne.jp です。
カレンダー
| 09 | 2025/10 | 11 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
最新コメント
[enken 02/23]
[中村東樹 02/04]
[m、m 02/04]
[爺の姪 01/13]
[レンマ学(メタ数学) 01/02]
[m.m 10/12]
[爺の姪 10/01]
[あは♡ 09/20]
[Mr.サタン 09/20]
[Mr.サタン 09/20]
最新トラックバック
ブログ内検索
カウンター
