瘋癲爺 拙痴无の戯言・放言・歯軋り
12月21日の新聞に「数学の極意 インドで聞いた」という記事が出出ていました。
そこでインドの計算法ついて調べてみました。①19×14
②27×23
次に、十の位が同じで、一の位の数の和が10になる場合を考えます。
例として、27と23の積を考えましょう。
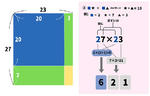
ここで、青い部分の面積は、20×20=400
緑の部分の面積は(3+7)×20=200
ここでは一の位の数の和が10になる場合を考えているので、緑の面積は常に 十の位の数×100 になります。
よって青と緑の面積の和は、20×(20+10)=600
ここに黄色の面積 7×3=21を足します。
よって答えは、20×30+7×3=600+21=621
一般化すると、十の位が同じで一の位の数の和が10になる数同士のかけ算は、
{(十の位の数)×10}×{(十の位の数)+1)}×10+(一の位の数の積)
③62×42

そこでインドの計算法ついて調べてみました。
①19×14
まずは、十の位でくくって考えるやり方です。
インド式計算法の基本の考え方です。
例として、19×14を考えてみましょう。
まず、19を10と9、14を10と4に分けて考えます。
イメージ図は以下です。

ここで、青い部分の面積は19×10+10×4だから、(19+4)×10=230
そこに、黄色い部分の面積 9×4=36を足します。
よって答えは、(19+4)×10+36=230+36=266
ちなみに、ひっくり返して14×10+10×9としても、(14+9)×10+36=230でやはり答えは230になります。
一般化すると、十の位が同じ数同士のかけ算は、一般化すると、十の位が同じ数同士のかけ算は、
{(一方の数)+(他方の数の一の位)}×(十の位の数×10)+(一の位の数の積)
<例>
• 13×15=(13+5)×10+3×5=180+15=195
• 17×14=(17+4)×10+7×4=210+28=238
• 25×27=(25+7)×20+5×7=640+35=675
• 32×34=(32+4)×30+2×4=1080+8=1088
②27×23
次に、十の位が同じで、一の位の数の和が10になる場合を考えます。
例として、27と23の積を考えましょう。
ここで、青い部分の面積は、20×20=400
緑の部分の面積は(3+7)×20=200
ここでは一の位の数の和が10になる場合を考えているので、緑の面積は常に 十の位の数×100 になります。
よって青と緑の面積の和は、20×(20+10)=600
ここに黄色の面積 7×3=21を足します。
よって答えは、20×30+7×3=600+21=621
一般化すると、十の位が同じで一の位の数の和が10になる数同士のかけ算は、
{(十の位の数)×10}×{(十の位の数)+1)}×10+(一の位の数の積)
<例>
• 34×36=30×40+4×6=1200+24=1224
• 47×43=40×50+7×3=2000+21=2021
• 61×69=60×70+1×9=4200+9=4209
③62×42
次に、十の位の数の和が10で、一の位が同じ場合を考えます。
例として、62×42を考えましょう。
ここで、青い部分の面積は60×40=2400
緑の部分の面積は(60+40)×2=200
十の位の数の和が10になる場合を考えているので、緑の面積は常に (一の位の数)×100 になります。
ここに黄色の面積 2×2=4を足します。
よって答えは、60×40+200+2×2=2400+200+4=2604
一般化すると、十の位の数の和が10で、一の位が同じ数同士のかけ算は、
{
×100+(一の位の数の積)
PR
この記事にコメントする
プロフィール
ハンドルネーム:
目高 拙痴无
年齢:
93
誕生日:
1932/02/04
自己紹介:
くたばりかけの糞爺々です。よろしく。メールも頼むね。
sechin@nethome.ne.jp です。
sechin@nethome.ne.jp です。
カレンダー
| 10 | 2025/11 | 12 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
最新コメント
[enken 02/23]
[中村東樹 02/04]
[m、m 02/04]
[爺の姪 01/13]
[レンマ学(メタ数学) 01/02]
[m.m 10/12]
[爺の姪 10/01]
[あは♡ 09/20]
[Mr.サタン 09/20]
[Mr.サタン 09/20]
最新トラックバック
ブログ内検索
カウンター
