瘋癲爺 拙痴无の戯言・放言・歯軋り
円錐を1つの平面で切って得られる曲線を総称して円錐曲線と呼ぶが、この円錐曲線に関するApollonios(アポロニウス)の研究は詳細を極め、Apolloniosは円錐曲線の重要な性質のほとんどを知っていたらしい。たとえば、昨日のブログで定義された楕円は、2つの定点からの距離の和が一定な点の軌跡であることは次のようにして説明されている。
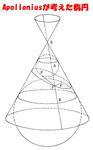 いま、1つの直円錐を1つの平面で切ってその切り口に楕円が得られている場合、この直円錐に内接して、しかもこの切り口にも接する球を考えれば、その様な球は2つある。これらの球と、切り口との接点を左図のようにそれぞれF、F’とする。これらの球は直円錐とそれぞれ1つの円に沿って接している。
いま、1つの直円錐を1つの平面で切ってその切り口に楕円が得られている場合、この直円錐に内接して、しかもこの切り口にも接する球を考えれば、その様な球は2つある。これらの球と、切り口との接点を左図のようにそれぞれF、F’とする。これらの球は直円錐とそれぞれ1つの円に沿って接している。
今楕円上に勝手な1点Pを取り、直円錐の頂点Sと点Pを結ぶ直線がこれらの円と交わる点をそれぞれA、Bとすれば、PFとPAとは、共に1点Pから1つの球に引いた接線の長さであるから、その長さは等しく、
PF=PA …… (1)
また、PF’とPBとも、ともに1点Pから1つの球へ引いた接線の長さであるから、その長さは等しく、
PF’=PB …… (2)
(1)と(2)の辺々を加えれば、 PF+PF’=AB
ところが、ABの長さはPを楕円状のどこにとっても一定である。したがって、楕円上の任意の1点Pから、2つの定点F、F’にいたる距離の和はいつも一定である。
なお、Apollonios(アポロニウス)は2つの定点AとBにいたる距離の比が一定値 m:n であるような点Pの軌跡を研究した。
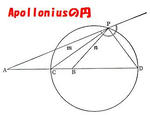 いま、∠APB を2等分する直線が直線ABと交わる点をCとすれば、Cは線分ABを m:n に内分する点である。したがって、点Cは定点である。
いま、∠APB を2等分する直線が直線ABと交わる点をCとすれば、Cは線分ABを m:n に内分する点である。したがって、点Cは定点である。
また、∠APBの外角を2等分する直線が直線ABと交わる点をDとすれば、Dは線分ABを m:n に外分する点である。したがって、点Dも定点である。
ところで、上の作図に拠れば、∠CPDは直角である。したがって、点Pは一定の線分CDを直径とする一定の円周上にある。
この円は「Apollonios(アポロニウス)の円」と呼ばれている。高校の幾何で習った方もいらっしゃると思う。
今楕円上に勝手な1点Pを取り、直円錐の頂点Sと点Pを結ぶ直線がこれらの円と交わる点をそれぞれA、Bとすれば、PFとPAとは、共に1点Pから1つの球に引いた接線の長さであるから、その長さは等しく、
PF=PA …… (1)
また、PF’とPBとも、ともに1点Pから1つの球へ引いた接線の長さであるから、その長さは等しく、
PF’=PB …… (2)
(1)と(2)の辺々を加えれば、 PF+PF’=AB
ところが、ABの長さはPを楕円状のどこにとっても一定である。したがって、楕円上の任意の1点Pから、2つの定点F、F’にいたる距離の和はいつも一定である。
なお、Apollonios(アポロニウス)は2つの定点AとBにいたる距離の比が一定値 m:n であるような点Pの軌跡を研究した。
また、∠APBの外角を2等分する直線が直線ABと交わる点をDとすれば、Dは線分ABを m:n に外分する点である。したがって、点Dも定点である。
ところで、上の作図に拠れば、∠CPDは直角である。したがって、点Pは一定の線分CDを直径とする一定の円周上にある。
この円は「Apollonios(アポロニウス)の円」と呼ばれている。高校の幾何で習った方もいらっしゃると思う。
PR
この記事にコメントする
プロフィール
ハンドルネーム:
目高 拙痴无
年齢:
93
誕生日:
1932/02/04
自己紹介:
くたばりかけの糞爺々です。よろしく。メールも頼むね。
sechin@nethome.ne.jp です。
sechin@nethome.ne.jp です。
カレンダー
| 07 | 2025/08 | 09 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 |
最新コメント
[enken 02/23]
[中村東樹 02/04]
[m、m 02/04]
[爺の姪 01/13]
[レンマ学(メタ数学) 01/02]
[m.m 10/12]
[爺の姪 10/01]
[あは♡ 09/20]
[Mr.サタン 09/20]
[Mr.サタン 09/20]
最新トラックバック
ブログ内検索
カウンター
