瘋癲爺 拙痴无の戯言・放言・歯軋り
アポロニウスの問題 (Apollonius' problem) は、平面上の任意の 3 つの円に正接する円を作図するというユークリッド平面幾何学における難問として有名である。Perga[ペルガ、トルコ南部の都市]のApollonius(アポロニウス)が、自著の『接触』 (“Tangencies”)2巻で提起し、解決した有名な問題という。この著作自体は失われたが、その解法を示した、4 世紀のAlexandria(アレキサンドリア)のPappus (パップス、AD320年ごろ) の記録が残っているという。
問題は『接触』の中で、次のように表現されていたという。「3つのものが与えられていて、その各々は点、直線、円のいずれかである。与えられたものが点のときには、その点を通る円、与えられたものが直線または円のときは、それに接する、という条件を満足する円を描け」というものである。
これは1つの表現で、色々な場合うを含ませているので、判りにくいが、たとえば、点、直線、円が与えられているときは、その点を通り、その直線と円に接する円を描けという問題になる。また、2点と1直線の組み合わせの時は、2点を通ってその直線に接する円を描けという問題になる。
三つのものの与え方には10の異なる場合がある。
(1)3点、(2)3直線、(3)2点と1直線、(4)2直線と1点、(5)2点と1円、
(6)2円と1点、(7)2直線と1円、(8)2円と1直線、(9)1点と1直線と1円、(10)3円
の10通りがある。このうち、(1)は3点を通る円、(2)は3直線に接する円で、これらはEukleides(エウクレイデス)の『原論』ですでに扱われている。(3)、(4)、(5)、(6)、(8)、(9)の六つは『接触』の第1巻で扱われ、(7)すなわち2直線と円の場合と、(10)3円の場合は『接触』の第2巻の全てを占めているという。
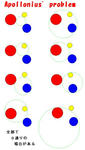 アポロニウスの問題は元来、上の10個の場合の全部を含むものであるが、通常は狭義の意味で最後の(10)を指す。いやはや、(10)の場合、すなわち3円に接する円ににしても、左図に示すように、これだけでも8通りの場合があるのである。
アポロニウスの問題は元来、上の10個の場合の全部を含むものであるが、通常は狭義の意味で最後の(10)を指す。いやはや、(10)の場合、すなわち3円に接する円ににしても、左図に示すように、これだけでも8通りの場合があるのである。
これらの 8 つの円は、おのおの与えられた 3 つの円と互いに異なる方法で内接または外接する。 Francois Viete (フランソワ・ビエト、1540~1603年、フランスの法律家、数学者) はこれに極限値を用い、与えられた 3つの円のいずれかを半径ゼロ (即ち、「点」) まで縮小し、または半径無限大 (「直線」) に拡大する解法を考え出した。単純化した例を用いて複雑な問題を解決するViete(ビエト)の解法は、Apollonius(アポロニウス)を再構成したものとして妥当であるとされている。
問題は『接触』の中で、次のように表現されていたという。「3つのものが与えられていて、その各々は点、直線、円のいずれかである。与えられたものが点のときには、その点を通る円、与えられたものが直線または円のときは、それに接する、という条件を満足する円を描け」というものである。
これは1つの表現で、色々な場合うを含ませているので、判りにくいが、たとえば、点、直線、円が与えられているときは、その点を通り、その直線と円に接する円を描けという問題になる。また、2点と1直線の組み合わせの時は、2点を通ってその直線に接する円を描けという問題になる。
三つのものの与え方には10の異なる場合がある。
(1)3点、(2)3直線、(3)2点と1直線、(4)2直線と1点、(5)2点と1円、
(6)2円と1点、(7)2直線と1円、(8)2円と1直線、(9)1点と1直線と1円、(10)3円
の10通りがある。このうち、(1)は3点を通る円、(2)は3直線に接する円で、これらはEukleides(エウクレイデス)の『原論』ですでに扱われている。(3)、(4)、(5)、(6)、(8)、(9)の六つは『接触』の第1巻で扱われ、(7)すなわち2直線と円の場合と、(10)3円の場合は『接触』の第2巻の全てを占めているという。
これらの 8 つの円は、おのおの与えられた 3 つの円と互いに異なる方法で内接または外接する。 Francois Viete (フランソワ・ビエト、1540~1603年、フランスの法律家、数学者) はこれに極限値を用い、与えられた 3つの円のいずれかを半径ゼロ (即ち、「点」) まで縮小し、または半径無限大 (「直線」) に拡大する解法を考え出した。単純化した例を用いて複雑な問題を解決するViete(ビエト)の解法は、Apollonius(アポロニウス)を再構成したものとして妥当であるとされている。
PR
この記事にコメントする
プロフィール
ハンドルネーム:
目高 拙痴无
年齢:
93
誕生日:
1932/02/04
自己紹介:
くたばりかけの糞爺々です。よろしく。メールも頼むね。
sechin@nethome.ne.jp です。
sechin@nethome.ne.jp です。
カレンダー
| 07 | 2025/08 | 09 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 |
最新コメント
[enken 02/23]
[中村東樹 02/04]
[m、m 02/04]
[爺の姪 01/13]
[レンマ学(メタ数学) 01/02]
[m.m 10/12]
[爺の姪 10/01]
[あは♡ 09/20]
[Mr.サタン 09/20]
[Mr.サタン 09/20]
最新トラックバック
ブログ内検索
カウンター
