瘋癲爺 拙痴无の戯言・放言・歯軋り
Menaichmos(メナイクモス)は、例えば放物線に対して次のような考察を加えている。
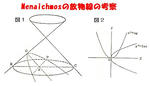 今、頂点における角の開きが直角であるような直円錐を1つの母線に垂直な平面で切って得られる放物線の頂点をOとし、その軸上の1点Aで、この切り口の平面内で軸に垂線を立て、放物線との交点をPとする(左図の図1)。このときPは、Aを通ってこの直円錐の軸に垂直な平面でこの直円錐を切った切り口の円上にある。いまAを通るこの円の直径をBCとすれば、 AP²=BA・AC である。
今、頂点における角の開きが直角であるような直円錐を1つの母線に垂直な平面で切って得られる放物線の頂点をOとし、その軸上の1点Aで、この切り口の平面内で軸に垂線を立て、放物線との交点をPとする(左図の図1)。このときPは、Aを通ってこの直円錐の軸に垂直な平面でこの直円錐を切った切り口の円上にある。いまAを通るこの円の直径をBCとすれば、 AP²=BA・AC である。
ところが、 BA:OA は一定であるから、kを定数として、 BA=k・OA と置くことができる。
したがって、上の式は AP²=(k・AC)・OA と書かれる。ところが、kもACも一定であるから、k・AC をℓと置けば、 AP²=ℓ・OA となる。
これは、現代流に言えば、放物線の頂点を原点、軸をx軸にとれば、 y²=ℓx …… 放物線の方程式
であるということである。
Menaichmos(メナイクモス)は
2つの放物線 y²=2ax、 x²=ay の原点以外のx座標が x³=2a³ を満たすことをりようして、デロスの問題を解いたといわれる。(左図の図2参照)
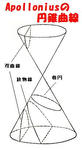 さて、Apollonios(アポロニウス)は、Menaichmos(メナイクモス)のように種々の直円錐をその1つの母線に垂直な平面できる代わりに、ただ1つの円錐を種々の平面で切った。
さて、Apollonios(アポロニウス)は、Menaichmos(メナイクモス)のように種々の直円錐をその1つの母線に垂直な平面できる代わりに、ただ1つの円錐を種々の平面で切った。
そして、この平面が底面となす角が、母線が底面となす角より小さいか、それに等しいか、またはそれより大きいかにしたがって、上の現代流の標記にしたがえば、
y²=ℓx-ax²、 y²=ℓx、 y²=ℓx+ax² であることを示した。ただし、ℓは一定の長さ、aは一定の数である。(左図参照)
Apollonios(アポロニウス)は、ここに、 y²<ℓx、 y²=ℓx、 y²>ℓx であることに注目にして、
これらをそれぞれ y²<ℓx → 不足する(ellipsis エリプシス)、
y²=ℓx → 一致する(parabole パラボル)、
y²>ℓx → 超越する(hyperbole ハイパーボル) と呼んだという。これが
Ellipse〔エリブス、楕円〕 parabola〔パラボラ、放物線〕 hyperbola〔ハイパーボラ、双曲線〕 の語源となっているのであるという。
ところが、 BA:OA は一定であるから、kを定数として、 BA=k・OA と置くことができる。
したがって、上の式は AP²=(k・AC)・OA と書かれる。ところが、kもACも一定であるから、k・AC をℓと置けば、 AP²=ℓ・OA となる。
これは、現代流に言えば、放物線の頂点を原点、軸をx軸にとれば、 y²=ℓx …… 放物線の方程式
であるということである。
Menaichmos(メナイクモス)は
2つの放物線 y²=2ax、 x²=ay の原点以外のx座標が x³=2a³ を満たすことをりようして、デロスの問題を解いたといわれる。(左図の図2参照)
そして、この平面が底面となす角が、母線が底面となす角より小さいか、それに等しいか、またはそれより大きいかにしたがって、上の現代流の標記にしたがえば、
y²=ℓx-ax²、 y²=ℓx、 y²=ℓx+ax² であることを示した。ただし、ℓは一定の長さ、aは一定の数である。(左図参照)
Apollonios(アポロニウス)は、ここに、 y²<ℓx、 y²=ℓx、 y²>ℓx であることに注目にして、
これらをそれぞれ y²<ℓx → 不足する(ellipsis エリプシス)、
y²=ℓx → 一致する(parabole パラボル)、
y²>ℓx → 超越する(hyperbole ハイパーボル) と呼んだという。これが
Ellipse〔エリブス、楕円〕 parabola〔パラボラ、放物線〕 hyperbola〔ハイパーボラ、双曲線〕 の語源となっているのであるという。
PR
この記事にコメントする
プロフィール
ハンドルネーム:
目高 拙痴无
年齢:
93
誕生日:
1932/02/04
自己紹介:
くたばりかけの糞爺々です。よろしく。メールも頼むね。
sechin@nethome.ne.jp です。
sechin@nethome.ne.jp です。
カレンダー
| 07 | 2025/08 | 09 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 |
最新コメント
[enken 02/23]
[中村東樹 02/04]
[m、m 02/04]
[爺の姪 01/13]
[レンマ学(メタ数学) 01/02]
[m.m 10/12]
[爺の姪 10/01]
[あは♡ 09/20]
[Mr.サタン 09/20]
[Mr.サタン 09/20]
最新トラックバック
ブログ内検索
カウンター
