瘋癲爺 拙痴无の戯言・放言・歯軋り
Cleomedes(クレオメデス)によれば、Eratosthenes(エラトステネス)は、Syene(シエネ)とAlexandria(アレキサンドリア)の距離を当時の単位で5000スタディアと見積り、ここから比率計算で地球の全周長は 50×5000、すなわち 250 000 stadia〔スタディア〕と求めた(左図参照)。 一方、Eratosthenes(エラトステネス)を伝える他の多くの著者は、252 000 stadiaという値を与えている。 多くの研究者は後者の値をエラトステネスが元々の値にさらに2000 stadiaを加えて修正を行ったためだと考えている。 その理由は明らかではないが、正確性より実用性を重んじたため、単に当時用いられていた円周の60分割単位(すなわち角度の 6°単位)あたりの距離を切りよく4200 stadiaとするためであったという説がある。 また、Syene(シエネ)とAlexandria(アレキサンドリア)との距離は直接にはEratosthenes(エラトステネス)が作成した地図から得たものと考えられるが、それが元々どのようにもたらされた値であるかについてはわかっていない。しかしStrábôn(ストラボン、BC63?~23?年、古代ローマ時代のギリシア系の地理学者・歴史家・哲学者)はナイルが毎年氾濫を起し地形を変えるために、エジプトでは専門の歩行者を使って毎年繰り返し距離の測定を行っていたことを記述している。
このEratosthenes(エラトステネス)が求めた地球の大きさの値が現在の単位でどれだけであるかについては議論が分かれている。stadion 〔スタディオン、スタディアの単数形〕の大きさは時代や場所によって異なっており、エラトステネスが用いたstadion(スタディオン)の現在の単位での値ははっきりしていない。 もっとも広く知られている天文学者Dennis Rawlins〔デニス・ローリンズ、1937~ 、アメリカの天文学者〕の説では、1 stadion(スタディオン)は185メートルであるとされ、このとき 252 000 stadiaは地球の全周長よりおよそ 17 % 大きな 46 250 キロメートルとなる。 しかし歴史学者Carl Ferdinand Friedrich Lehmann―Haupt〔カール・フリードリヒ・レーマン=ハウプト、1861~1938年、ドイツの歴史学者〕は、stadion(スタディオン)には少なくとも6種類のものがあったと主張している。
いずれにしても地球が球体であり、かつ太陽光が平行線であるという前提の元で、このEratosthenes(エラトステネス)の推論は幾何学的に正しいものであり、その精度の範囲内において得られた値もほぼ正しいものであった。オーストリアの科学史家Otto Neugebauer 〔オットー・ノイゲバウアー、1899~1990年〕 によれば、元々この値は「距離の『測定』も天文学的『観測』も大雑把な見積もり以上のものではなく、扱いやすい概数値として表されたものであることが明らか」なものであった。なお、地球の大きさの実質的な最初の測定は10世紀アラビアの天文学者 al-Bīrūnī〔アル=ビールーニー、973~1048年)によって行われている。
PR
地球の大きさを初めて測定した人物として、また素数の判定法であるエラトステネスの篩(ふるい)を発明したことで知られる。その業績から(第2のプラトン」とも呼ばれた。また「β(ベータ)」ともあだ名されている。その由来は、「世界で2番目に物事をよく知っている人」という意味であるらしい。ここでは1番の人は「α(アルファ)」と呼ばれることになる。
BC255年ごろには初の天球儀を作成した。 Cleomedes(クレオメデス、生没年不詳BC1世紀頃、ストア派の哲学者、天体学者)の『天体の回転運動について』によれば、紀元前240年ごろに、Syene〔シエネ、現在のAswan(アスワン)〕のそばのElephantine(エレファンティン) 島とAlexandria(アレキサンドリア)とでの夏至の正午の太陽高度の知識を元に地球の全周を計算している。 この地球の大きさの測定に関してエラトステネス自身の著述は残されていないが、Cleomedes(クレオメデス)を初め、Strabo(ストラボン、BC63~23年頃、古代ローマ時代のギリシア系の地理学者・歴史家・哲学者)、Claudius Ptolemaios〔クラウディオス・プトレマイオス、AD150年ごろ〕など多くの後世の学者によって言及されている。
紀元前236年、プトレマイオス3世によってApollōnios Rhodios(ロドスのアポローニオス、BC3世紀初期~紀元前246年以降、叙事詩人、学者、アレクサンドリア図書館長)の後任としてアレクサンドリア図書館の館長に任命され、少なくとも紀元前204年までその地位にあった。 紀元前195年には目が不自由となり、翌年82歳で没した。
現代に残っているAristarchus(アリスタルコス)の唯一の著作である『太陽と月の大きさと距離について』は地球中心説(天動説)の世界観に基づくものである。しかし、記録に残されている引用句を通じて、Aristarchus(アリスタルコス)がこれに代わる太陽中心説の仮説を提唱した別の書物を著していたことが明らかになっている。Pappus(パップス)の論文集「小天文学」に収録されている。10世紀ごろにアラビア語に翻訳されており、15世紀ごろにラテン語訳が刊行された。ギリシア語のテキストは1700年ごろに出版された。1800年ごろにフランス語訳およびドイツ語訳が出版された。Archimedes(アルキメデス)は小文『砂粒を数えるもの』の中で以下のように書いている。
「ゲロン王陛下は、『宇宙』という語は多くの天文学者によって、地球の中心をその中心とし、太陽の中心と地球の中心を結ぶ直線をその半径とする球に対して付けられた名称であることをご存知でしょう。この説明は、陛下が天文学者たちからお聞きになったのと同様、一般によく知られております。しかしAristarchus(アリスタルコス)はある本の中で、いくつかの仮定から導かれる帰結として、宇宙は先ほど述べました「宇宙」よりも何倍も大きいとの仮説を提唱しております。彼の仮説によれば、恒星と太陽は不動で、地球は太陽の周囲のある円周上を回転し、太陽はその軌道の中ほどに位置します。恒星天球の中心は太陽とほぼ同じ位置にあり、その大きさは非常に大きく、地球が回転するという円の大きさと恒星までの距離の比は、恒星天球の中心までの距離と天球表面までの距離の比に等しくなると言います。」
Aristarchus(アリスタルコス)はこのように、恒星はほぼ無限に遠い距離にあると考えていた。彼はまたこのことが、恒星に視差(地球が太陽の周囲を公転することで恒星の見かけの位置が変化する現象)が見られない理由であると考えた。実際、恒星までの距離は古代に考えられていたよりもはるかに大きいため、恒星の視差は望遠鏡を使わなければ検出することができない。しかし地球中心説はより単純な仮定に基づいており、視差が観測されない理由についても(地球が不動だから、という)より明確な説明を与える。このため、太陽中心説に対する反発は非常に強いものとなった。例として、Plutarchus(プルタルコス)は以下のように書いているという。
「(Aristarchusと同時代のストア派哲学者Cleanthes〔クレアンテス、BC 331?―232?年〕は、)ギリシャ市民には、宇宙の中心(地球)を動かし、……天が不動である一方で、地球は自らの軸の周りを自転すると同時に傾いた円の上を周回する、などと想像した不敬の罪でSamos(サモス)のAristarchus(アリスタルコス)を告発する義務がある、と考えた。」
Aristarchus(アリスタルコス)は、月が上弦または下弦の時には太陽と月と地球がほぼ直角三角形を作ると述べた。彼はこの時の地球から見た月と太陽の離角を約87度と見積もった。この値を用いれば三角形の幾何学から太陽までの距離を求めることができる。Aristarchus(アリスタルコス)は計算によって、太陽は月よりも約20倍遠い距離にあると結論した。実際には上弦または下弦の時の月の離角は約89度50分で、太陽は月よりも約390倍遠い距離にある。Aristarchus(アリスタルコス)が用いた幾何学は正しかったが、観測した離角の値があまり正確でなかった。また彼は、月と太陽は見かけの角直径がほぼ等しいため、両者の実際の直径は各々の地球からの距離に比例するはずだと指摘した。ここから彼は、太陽は月よりも20倍大きいという結論を観測データから論理的に導いた。この数値自体は観測が不正確だったために間違っていたが、この推論は太陽が地球よりも明らかに大きいことを示唆しており、太陽中心説を支持する材料となりうるものだった。
Alexander 大王〔アレキサンダー、BC356~323年、在位BC336~323年)は、世界征服を企て、東はインドから西はイタリアにいたる三大国家〔アンティゴノス朝マケドニア、セレウコス朝シリア、プトレマイオス朝エジプトのヘレニズム三王国〕を建設した。彼は武力と政治のみをこととせず、文化の発展にも意を注いだので、ギリシア文化を他国へ移すとともに、東洋的文化をギリシア文化に加えることにも貢献した。こうして出来上がったのが、ヘレニズム文化である。
 Alexander 大王の死後はさしもの大国家も分裂してしまったが、エジプトはPtolemaios(プトレマイオス)によって受け継がれ、その都Alexandria(アレキサンドリア)は長く文化の中心として栄えた。
Alexander 大王の死後はさしもの大国家も分裂してしまったが、エジプトはPtolemaios(プトレマイオス)によって受け継がれ、その都Alexandria(アレキサンドリア)は長く文化の中心として栄えた。
この時代の数学者として先ず挙げられるのはEukleides(エウクレイデス、BC300年ごろ、英語読みではEuclid)である。かれは、それまでに知られていたすべての数学に再検討を加えて、Elements(原本)とよばれる全13の大著を書いたことで知られる。
次に挙げられるべきは当時の数学者、科学者Archimedes(アルキメデス、BC287~212年)であろう。彼は円の面積、球の体積、表面積を研究し、円周率の近似値を小数第2位までもとめた歴史上最初の人であったばかりでなく、実用的な発明も数々残していることは、ブログに取上げたとおりである。
また、つい先日までに取上げたApollonius(アポロニウス、BC200年頃)の名前も逸してはならない。
この辺りまでを、Alexandria(アレキサンドリア)前期と呼ぶならば、後期の時代には、東西交通はますます盛んとなり、それにつれて航海術のなどの必要から、天文学と三角法が研究された。
天文学は単なる空想から離れて、観測を取上げることによって、Aristarchos〔アリスタルコス、BC28年ごろ〕、Eratosrhenes〔エラトステネス、BC275~194年〕を経て、Hipparchus〔ヒッパルコス、BC150年ごろ〕に至ってはじめて軌道に乗った。
また、このころの数学者しには、ヘロンの公式で有名なHeron〔ヘロン、BC100ねんごろ〕、メネラウスの定理で知られるMenelaus〔メネラウス、BC100年ごろ〕、トレミーの定理で有名なPtolemaios〔プトレマイオス、AD150年ごろ〕、それにディオファントス方程式で知られるDiophantos〔ディオファントス、AD300年ごろ〕、さらにパップスの定理でしられるPappus〔パップス、4世紀前半に活躍〕などがある。
この時代の数学者として先ず挙げられるのはEukleides(エウクレイデス、BC300年ごろ、英語読みではEuclid)である。かれは、それまでに知られていたすべての数学に再検討を加えて、Elements(原本)とよばれる全13の大著を書いたことで知られる。
次に挙げられるべきは当時の数学者、科学者Archimedes(アルキメデス、BC287~212年)であろう。彼は円の面積、球の体積、表面積を研究し、円周率の近似値を小数第2位までもとめた歴史上最初の人であったばかりでなく、実用的な発明も数々残していることは、ブログに取上げたとおりである。
また、つい先日までに取上げたApollonius(アポロニウス、BC200年頃)の名前も逸してはならない。
この辺りまでを、Alexandria(アレキサンドリア)前期と呼ぶならば、後期の時代には、東西交通はますます盛んとなり、それにつれて航海術のなどの必要から、天文学と三角法が研究された。
天文学は単なる空想から離れて、観測を取上げることによって、Aristarchos〔アリスタルコス、BC28年ごろ〕、Eratosrhenes〔エラトステネス、BC275~194年〕を経て、Hipparchus〔ヒッパルコス、BC150年ごろ〕に至ってはじめて軌道に乗った。
また、このころの数学者しには、ヘロンの公式で有名なHeron〔ヘロン、BC100ねんごろ〕、メネラウスの定理で知られるMenelaus〔メネラウス、BC100年ごろ〕、トレミーの定理で有名なPtolemaios〔プトレマイオス、AD150年ごろ〕、それにディオファントス方程式で知られるDiophantos〔ディオファントス、AD300年ごろ〕、さらにパップスの定理でしられるPappus〔パップス、4世紀前半に活躍〕などがある。
O、Q、O₂;O、R、O₃は、それぞれ1直線上にある。QRと円O₃の第2の交点をSとする。
以下、左図を参照
よって、Dは定点である。円O₃について考えてみると、三角形RTSはこれに内接する三角形で、RS、RT、STはそれぞれ定点C₁、C₂、Dを通り、これらは1直線上にある。したがってPappusの補題によって、この三角形は作図でき、したがって円Oも作図できる。
アポロニウスの問題 (Apollonius' problem) は、平面上の任意の 3 つの円に正接する円を作図するというユークリッド平面幾何学における難問として有名である。Perga[ペルガ、トルコ南部の都市]のApollonius(アポロニウス)が、自著の『接触』 (“Tangencies”)2巻で提起し、解決した有名な問題という。この著作自体は失われたが、その解法を示した、4 世紀のAlexandria(アレキサンドリア)のPappus (パップス、AD320年ごろ) の記録が残っているという。
問題は『接触』の中で、次のように表現されていたという。「3つのものが与えられていて、その各々は点、直線、円のいずれかである。与えられたものが点のときには、その点を通る円、与えられたものが直線または円のときは、それに接する、という条件を満足する円を描け」というものである。
これは1つの表現で、色々な場合うを含ませているので、判りにくいが、たとえば、点、直線、円が与えられているときは、その点を通り、その直線と円に接する円を描けという問題になる。また、2点と1直線の組み合わせの時は、2点を通ってその直線に接する円を描けという問題になる。
三つのものの与え方には10の異なる場合がある。
(1)3点、(2)3直線、(3)2点と1直線、(4)2直線と1点、(5)2点と1円、
(6)2円と1点、(7)2直線と1円、(8)2円と1直線、(9)1点と1直線と1円、(10)3円
の10通りがある。このうち、(1)は3点を通る円、(2)は3直線に接する円で、これらはEukleides(エウクレイデス)の『原論』ですでに扱われている。(3)、(4)、(5)、(6)、(8)、(9)の六つは『接触』の第1巻で扱われ、(7)すなわち2直線と円の場合と、(10)3円の場合は『接触』の第2巻の全てを占めているという。
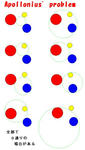 アポロニウスの問題は元来、上の10個の場合の全部を含むものであるが、通常は狭義の意味で最後の(10)を指す。いやはや、(10)の場合、すなわち3円に接する円ににしても、左図に示すように、これだけでも8通りの場合があるのである。
アポロニウスの問題は元来、上の10個の場合の全部を含むものであるが、通常は狭義の意味で最後の(10)を指す。いやはや、(10)の場合、すなわち3円に接する円ににしても、左図に示すように、これだけでも8通りの場合があるのである。
これらの 8 つの円は、おのおの与えられた 3 つの円と互いに異なる方法で内接または外接する。 Francois Viete (フランソワ・ビエト、1540~1603年、フランスの法律家、数学者) はこれに極限値を用い、与えられた 3つの円のいずれかを半径ゼロ (即ち、「点」) まで縮小し、または半径無限大 (「直線」) に拡大する解法を考え出した。単純化した例を用いて複雑な問題を解決するViete(ビエト)の解法は、Apollonius(アポロニウス)を再構成したものとして妥当であるとされている。
問題は『接触』の中で、次のように表現されていたという。「3つのものが与えられていて、その各々は点、直線、円のいずれかである。与えられたものが点のときには、その点を通る円、与えられたものが直線または円のときは、それに接する、という条件を満足する円を描け」というものである。
これは1つの表現で、色々な場合うを含ませているので、判りにくいが、たとえば、点、直線、円が与えられているときは、その点を通り、その直線と円に接する円を描けという問題になる。また、2点と1直線の組み合わせの時は、2点を通ってその直線に接する円を描けという問題になる。
三つのものの与え方には10の異なる場合がある。
(1)3点、(2)3直線、(3)2点と1直線、(4)2直線と1点、(5)2点と1円、
(6)2円と1点、(7)2直線と1円、(8)2円と1直線、(9)1点と1直線と1円、(10)3円
の10通りがある。このうち、(1)は3点を通る円、(2)は3直線に接する円で、これらはEukleides(エウクレイデス)の『原論』ですでに扱われている。(3)、(4)、(5)、(6)、(8)、(9)の六つは『接触』の第1巻で扱われ、(7)すなわち2直線と円の場合と、(10)3円の場合は『接触』の第2巻の全てを占めているという。
これらの 8 つの円は、おのおの与えられた 3 つの円と互いに異なる方法で内接または外接する。 Francois Viete (フランソワ・ビエト、1540~1603年、フランスの法律家、数学者) はこれに極限値を用い、与えられた 3つの円のいずれかを半径ゼロ (即ち、「点」) まで縮小し、または半径無限大 (「直線」) に拡大する解法を考え出した。単純化した例を用いて複雑な問題を解決するViete(ビエト)の解法は、Apollonius(アポロニウス)を再構成したものとして妥当であるとされている。
円錐を1つの平面で切って得られる曲線を総称して円錐曲線と呼ぶが、この円錐曲線に関するApollonios(アポロニウス)の研究は詳細を極め、Apolloniosは円錐曲線の重要な性質のほとんどを知っていたらしい。たとえば、昨日のブログで定義された楕円は、2つの定点からの距離の和が一定な点の軌跡であることは次のようにして説明されている。
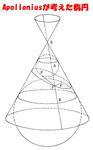 いま、1つの直円錐を1つの平面で切ってその切り口に楕円が得られている場合、この直円錐に内接して、しかもこの切り口にも接する球を考えれば、その様な球は2つある。これらの球と、切り口との接点を左図のようにそれぞれF、F’とする。これらの球は直円錐とそれぞれ1つの円に沿って接している。
いま、1つの直円錐を1つの平面で切ってその切り口に楕円が得られている場合、この直円錐に内接して、しかもこの切り口にも接する球を考えれば、その様な球は2つある。これらの球と、切り口との接点を左図のようにそれぞれF、F’とする。これらの球は直円錐とそれぞれ1つの円に沿って接している。
今楕円上に勝手な1点Pを取り、直円錐の頂点Sと点Pを結ぶ直線がこれらの円と交わる点をそれぞれA、Bとすれば、PFとPAとは、共に1点Pから1つの球に引いた接線の長さであるから、その長さは等しく、
PF=PA …… (1)
また、PF’とPBとも、ともに1点Pから1つの球へ引いた接線の長さであるから、その長さは等しく、
PF’=PB …… (2)
(1)と(2)の辺々を加えれば、 PF+PF’=AB
ところが、ABの長さはPを楕円状のどこにとっても一定である。したがって、楕円上の任意の1点Pから、2つの定点F、F’にいたる距離の和はいつも一定である。
なお、Apollonios(アポロニウス)は2つの定点AとBにいたる距離の比が一定値 m:n であるような点Pの軌跡を研究した。
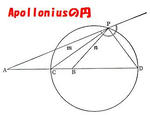 いま、∠APB を2等分する直線が直線ABと交わる点をCとすれば、Cは線分ABを m:n に内分する点である。したがって、点Cは定点である。
いま、∠APB を2等分する直線が直線ABと交わる点をCとすれば、Cは線分ABを m:n に内分する点である。したがって、点Cは定点である。
また、∠APBの外角を2等分する直線が直線ABと交わる点をDとすれば、Dは線分ABを m:n に外分する点である。したがって、点Dも定点である。
ところで、上の作図に拠れば、∠CPDは直角である。したがって、点Pは一定の線分CDを直径とする一定の円周上にある。
この円は「Apollonios(アポロニウス)の円」と呼ばれている。高校の幾何で習った方もいらっしゃると思う。
今楕円上に勝手な1点Pを取り、直円錐の頂点Sと点Pを結ぶ直線がこれらの円と交わる点をそれぞれA、Bとすれば、PFとPAとは、共に1点Pから1つの球に引いた接線の長さであるから、その長さは等しく、
PF=PA …… (1)
また、PF’とPBとも、ともに1点Pから1つの球へ引いた接線の長さであるから、その長さは等しく、
PF’=PB …… (2)
(1)と(2)の辺々を加えれば、 PF+PF’=AB
ところが、ABの長さはPを楕円状のどこにとっても一定である。したがって、楕円上の任意の1点Pから、2つの定点F、F’にいたる距離の和はいつも一定である。
なお、Apollonios(アポロニウス)は2つの定点AとBにいたる距離の比が一定値 m:n であるような点Pの軌跡を研究した。
また、∠APBの外角を2等分する直線が直線ABと交わる点をDとすれば、Dは線分ABを m:n に外分する点である。したがって、点Dも定点である。
ところで、上の作図に拠れば、∠CPDは直角である。したがって、点Pは一定の線分CDを直径とする一定の円周上にある。
この円は「Apollonios(アポロニウス)の円」と呼ばれている。高校の幾何で習った方もいらっしゃると思う。
Menaichmos(メナイクモス)は、例えば放物線に対して次のような考察を加えている。
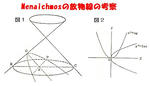 今、頂点における角の開きが直角であるような直円錐を1つの母線に垂直な平面で切って得られる放物線の頂点をOとし、その軸上の1点Aで、この切り口の平面内で軸に垂線を立て、放物線との交点をPとする(左図の図1)。このときPは、Aを通ってこの直円錐の軸に垂直な平面でこの直円錐を切った切り口の円上にある。いまAを通るこの円の直径をBCとすれば、 AP²=BA・AC である。
今、頂点における角の開きが直角であるような直円錐を1つの母線に垂直な平面で切って得られる放物線の頂点をOとし、その軸上の1点Aで、この切り口の平面内で軸に垂線を立て、放物線との交点をPとする(左図の図1)。このときPは、Aを通ってこの直円錐の軸に垂直な平面でこの直円錐を切った切り口の円上にある。いまAを通るこの円の直径をBCとすれば、 AP²=BA・AC である。
ところが、 BA:OA は一定であるから、kを定数として、 BA=k・OA と置くことができる。
したがって、上の式は AP²=(k・AC)・OA と書かれる。ところが、kもACも一定であるから、k・AC をℓと置けば、 AP²=ℓ・OA となる。
これは、現代流に言えば、放物線の頂点を原点、軸をx軸にとれば、 y²=ℓx …… 放物線の方程式
であるということである。
Menaichmos(メナイクモス)は
2つの放物線 y²=2ax、 x²=ay の原点以外のx座標が x³=2a³ を満たすことをりようして、デロスの問題を解いたといわれる。(左図の図2参照)
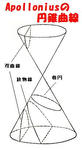 さて、Apollonios(アポロニウス)は、Menaichmos(メナイクモス)のように種々の直円錐をその1つの母線に垂直な平面できる代わりに、ただ1つの円錐を種々の平面で切った。
さて、Apollonios(アポロニウス)は、Menaichmos(メナイクモス)のように種々の直円錐をその1つの母線に垂直な平面できる代わりに、ただ1つの円錐を種々の平面で切った。
そして、この平面が底面となす角が、母線が底面となす角より小さいか、それに等しいか、またはそれより大きいかにしたがって、上の現代流の標記にしたがえば、
y²=ℓx-ax²、 y²=ℓx、 y²=ℓx+ax² であることを示した。ただし、ℓは一定の長さ、aは一定の数である。(左図参照)
Apollonios(アポロニウス)は、ここに、 y²<ℓx、 y²=ℓx、 y²>ℓx であることに注目にして、
これらをそれぞれ y²<ℓx → 不足する(ellipsis エリプシス)、
y²=ℓx → 一致する(parabole パラボル)、
y²>ℓx → 超越する(hyperbole ハイパーボル) と呼んだという。これが
Ellipse〔エリブス、楕円〕 parabola〔パラボラ、放物線〕 hyperbola〔ハイパーボラ、双曲線〕 の語源となっているのであるという。
ところが、 BA:OA は一定であるから、kを定数として、 BA=k・OA と置くことができる。
したがって、上の式は AP²=(k・AC)・OA と書かれる。ところが、kもACも一定であるから、k・AC をℓと置けば、 AP²=ℓ・OA となる。
これは、現代流に言えば、放物線の頂点を原点、軸をx軸にとれば、 y²=ℓx …… 放物線の方程式
であるということである。
Menaichmos(メナイクモス)は
2つの放物線 y²=2ax、 x²=ay の原点以外のx座標が x³=2a³ を満たすことをりようして、デロスの問題を解いたといわれる。(左図の図2参照)
そして、この平面が底面となす角が、母線が底面となす角より小さいか、それに等しいか、またはそれより大きいかにしたがって、上の現代流の標記にしたがえば、
y²=ℓx-ax²、 y²=ℓx、 y²=ℓx+ax² であることを示した。ただし、ℓは一定の長さ、aは一定の数である。(左図参照)
Apollonios(アポロニウス)は、ここに、 y²<ℓx、 y²=ℓx、 y²>ℓx であることに注目にして、
これらをそれぞれ y²<ℓx → 不足する(ellipsis エリプシス)、
y²=ℓx → 一致する(parabole パラボル)、
y²>ℓx → 超越する(hyperbole ハイパーボル) と呼んだという。これが
Ellipse〔エリブス、楕円〕 parabola〔パラボラ、放物線〕 hyperbola〔ハイパーボラ、双曲線〕 の語源となっているのであるという。
Apollonios(アポロニウス)は小アジアの町Perga〔ペルガ、トルコ語ではPerge(ペルゲ)〕に生まれた。Alexandria(アレキサンドリア)でプトレマイオス3世およびプトレマイオス4世の時代に活躍した。現トルコのPergamon(ペルガモン)でしばらく暮らしたとされる。Alexandria(アレキサンドリア)で没した。月のアポロニウスクレーターはApolloniosにちなんで命名されたという。Archimedes(アルキメデス)より40年ほど後に活躍した数学者であるが、アレキサンドリアで研究し、後にこの地で教授となった。
Apolloniosの研究の内で最も有名なのは、円錐曲線の研究であって、彼はそれまでの研究を整理し、それに彼の研究を付け加えて有名な『円錐曲線論』を残した。円錐曲線に関する彼の仕事を述べる前にPlaton〔プラトン、BC427~347年、古代ギリシアの哲学者〕の友人でもあったMenaichmos〔メナイクモス、BC375~325年、Eudoxos《ユードクソス、BC409~369年》の門下〕の円錐曲線に関する仕事について述べておく。
Sophistēs(ソフィスト)たち、そしてプラトン学派の人びとは、
(1)任意に与えられた角を3等分すること (2)与えられた立方体の2倍の体積をもつ立方体を作図すること(立方体倍積問題、デロスの問題) (3)与えられた円と同じ面積をもつ正方形を作図すること(円積問題) という、いわゆる3大難問を研究したが、作図の方法を定規とコンパス、すなわち直線と円に限ったのでは、その解決が困難であることが次第に明らかになっていった。こうして人びとの目は次第に直線と円以外の曲線に向けられるようになっていった。
このような状勢の下で、Eudoxos(ユードクソス)門下でPlatonの友人であったMenaichmos(メナイクモス)は、円錐曲線の概念に達したのである。円錐曲線というのは、円錐を1つの平面で切ったときにその切り口に現われる曲線のことであるが、Menaichmosはとくに、円錐をその1つの母線に垂直な平面で切った切り口を考えた。
Archimedes(アルキメデス)の考えた立体が13種あり、それがアルキメデスの立体(Archimedean Solids)と呼ばれている。
 アルキメデスの立体 (Archimedean solid) とは、凸な一様多面体のうち、正多面体以外のものである。一様多面体の条件は、全ての面が正多角形で、頂点形状が合同(頂点に集まる正多角形の種類と順序が同じ)なことである。正多面体は除外するので、半正多面体の面は2種類以上の正多角形で構成される(左図参照)。
アルキメデスの立体 (Archimedean solid) とは、凸な一様多面体のうち、正多面体以外のものである。一様多面体の条件は、全ての面が正多角形で、頂点形状が合同(頂点に集まる正多角形の種類と順序が同じ)なことである。正多面体は除外するので、半正多面体の面は2種類以上の正多角形で構成される(左図参照)。
①切頂四面体:正四面体の4つの頂点を切り落とした形になっている。4つの正六角形と、4つの正三角形の合わせて6つの面でできている。頂点の形状(3,6,6)。
※頂点の形状(3,6,6)とは、1つの頂点に正3角形、正6角形、正6角形が集まって構成されているということである。
②立方八面体:正八面体の辺の中点を通るような正方形で、6個の頂点を切り落とした形になっている〔立方体から8個の正三角形を切り取ったとも考えられる〕。頂点の形状(3,4,3,4)
③切頂八面体:正八面体の6個の頂点を切り落とした形になっている。6個の正方形と,8個の正六角形の合わせて14個の面でできている。頂点の形状(4,6,6)
④切頂立方体:立方体の8個の頂点を切り落とした形になっている。6この正八角形と、8個の正三角形の合わせて14個の面でできている。頂点の形状(3,8,8)
⑤小菱形立方八面体:作り方は次のようにイメージで出来る。(1)まず立方体の12本の辺を削ぎ落とす。つまり面取りする。この場所が次の(2)の段階で12個の正方形になるのである。(2)元の立方体の8個の頂点があった場所を切り落と。すると8個の正三角形が出来る。(3)以上の切り落としで,元の立方体の6つの正方形がそのまま,大きさだけ小さくなって残る。(4)実際には,後に残る18個の正方形と8個の正三角形の辺の長さが同じになる必要があるので,簡単に切り落としてもきちんとした図形は得られない。18個の正方形と,8個の正三角形の合わせて26個の面がある。頂点の形状(3,4,4,4)
⑥大菱形立方八面体:作り方は次のようにイメージできる。(1)まず立方体の12本の辺を削ぎ落とす。つまり面取りする。この場所が次の(2)の段階で12個の正方形になるのである。(2)元の立方体の8個の頂点があった場所を切り落として、8個の正六角形を作る。(3)以上の切り落としで、元の立方体の6つの正方形の場所に6個の正八角形が残ることになる。(4)実際には、後に残る12個の正方形と8個の正六角形、6個の正八角形の辺の長さが同じになる必要があるので、簡単に切り落としてもきちんとした図形は得られない。頂点の形状(4,6,8)
⑦捩れ立方体:作り方は次のようにイメージで出来る。(1)まず立方体の6つの正方形を外側に引っ張り、6つの立方体をそれぞれの中心の周りにまわしてやる。ねじれた6つの正方形の間に隙間ができる。(2)正方形の頂点を適当に3個ずつ選んで結び正三角形を作っていく。6個の正方形と、32個の正三角形の合わせて38個の面がある。頂点の形状(3,3,3,3,4)
⑧小菱形二十面十二面体:構成は比較的容易である。正十二面体から始め,まず正十二面体の辺をすべてそぎ落とし、正十二面体の20個の頂点の位置に正三角形を、そして30本の辺の位置に正方形が出来るように調整する。実際は正十二面体の辺の1/3の長さの位置で辺をそぎ落とせば出来る。30個の正方形と、20個の正三角形、12個の正五角形の合わせて62個の面で出来ている。面の個数は大菱形二十面十二面体と同じ。頂点の形状(3,4,5,4)
⑨大菱形二十面十二面体:構成は二十面十二面体の30個の頂点を切り取ったような形であるが、切り取った辺りには長方形しか出来ないのでこの方法では30個の正方形が出来ない。正方形を作るには,正十二面体から始め,まず正十二面体の辺をすべてそぎ落とす。次に元の正十二面体の頂点周りを切り落とす。辺をそぎ落としたり,頂点周りを切り落とす幅を調節して正方形、正六角形、正十角形を作るのである。30個の正方形と、20個の正六角形、12個の正十角形の合わせて62個の面で出来ている。頂点の形状(4,6,10)
⑩切頂二十面体:構成は他の切頂四面体や切頂立方体、切頂十二面体などと同様に頂点を切り落とすだけなのでイメージしやすい。正二十面体の12個の頂点を切り落とした形に鳴っている。20個の正六角形と、12個の正五角形の合わせて32個の面でできている。頂点の形状は(5,6,6)
 これは、実はあの有名なサッカーボールなのである。サッカーボールといっても古典的なもので、例の白い六角形と黒い五角形のもので〔左の写真左〕、1960年代以来親しまれているものである。ワールドカップでは,アディダス社が1970年のメキシコ大会から提供した者で、テルスター(Telstar) というブランド名での生産だったとされている。切頂二十面体をもとにしたデザインであり,つまり正二十面体がその最も基礎の図形です。他方,最近のワールドカップや大きな大会では違ったデザインのものが使用されているようです〔左の写真の右〕。2006年のワールドカップ・ドイツ大会以来用いられているということである。アディダス社の提供球で、+Teamgeist (プラスティームガイスト)というブランド名のボールだそうである。これはどうも見た目切頂二十面体の観点からは,ちょっと違和感を感じてしまう。
これは、実はあの有名なサッカーボールなのである。サッカーボールといっても古典的なもので、例の白い六角形と黒い五角形のもので〔左の写真左〕、1960年代以来親しまれているものである。ワールドカップでは,アディダス社が1970年のメキシコ大会から提供した者で、テルスター(Telstar) というブランド名での生産だったとされている。切頂二十面体をもとにしたデザインであり,つまり正二十面体がその最も基礎の図形です。他方,最近のワールドカップや大きな大会では違ったデザインのものが使用されているようです〔左の写真の右〕。2006年のワールドカップ・ドイツ大会以来用いられているということである。アディダス社の提供球で、+Teamgeist (プラスティームガイスト)というブランド名のボールだそうである。これはどうも見た目切頂二十面体の観点からは,ちょっと違和感を感じてしまう。
⑪切頂十二面体:構成は他の切頂四面体や切頂立方体などと同様に頂点を切り落とすだけなのでイメージしやすい。正十二面体の20個の頂点を切り落とした形になっている。12個の正十角形と,20個の正三角形の合わせて32個の面でできている。頂点の形状(3,10,10)
⑫二十面十二面体:構成は切頂十二面体や切頂二十面体と似ている。まず正十二面体のそれぞれの辺の中点を結んで正三角形を20個作れば出来る。または正二十面体のそれぞれの辺の中点を結んでできた正五角形で頂点を切っていけば出来上がる。20個の正三角形と,12個の正五角形の合わせて32個の面で出来ている。頂点の形状(3,5,3,5)
⑬捩れ十二面体:正十二面体から始め、先ず正十二面体の各面を縮小して辺が約0.56倍になるようにする。次にそれぞれの正五角形をその中心の回りに約13°回転してやる。出来上がった正五角形の頂点を正三角形ができるように結べば出来上がる。
 正十二面体と、小菱形二十面十二面体、それに捩れ十二面体の図を並べて見ると分かりやすいかと思う(左図参照)。12個の正五角形と、80個の正三角形の合わせて92個の面で出来ている。頂点の形状(3,3,3,3,5)
正十二面体と、小菱形二十面十二面体、それに捩れ十二面体の図を並べて見ると分かりやすいかと思う(左図参照)。12個の正五角形と、80個の正三角形の合わせて92個の面で出来ている。頂点の形状(3,3,3,3,5)
①切頂四面体:正四面体の4つの頂点を切り落とした形になっている。4つの正六角形と、4つの正三角形の合わせて6つの面でできている。頂点の形状(3,6,6)。
※頂点の形状(3,6,6)とは、1つの頂点に正3角形、正6角形、正6角形が集まって構成されているということである。
②立方八面体:正八面体の辺の中点を通るような正方形で、6個の頂点を切り落とした形になっている〔立方体から8個の正三角形を切り取ったとも考えられる〕。頂点の形状(3,4,3,4)
③切頂八面体:正八面体の6個の頂点を切り落とした形になっている。6個の正方形と,8個の正六角形の合わせて14個の面でできている。頂点の形状(4,6,6)
④切頂立方体:立方体の8個の頂点を切り落とした形になっている。6この正八角形と、8個の正三角形の合わせて14個の面でできている。頂点の形状(3,8,8)
⑤小菱形立方八面体:作り方は次のようにイメージで出来る。(1)まず立方体の12本の辺を削ぎ落とす。つまり面取りする。この場所が次の(2)の段階で12個の正方形になるのである。(2)元の立方体の8個の頂点があった場所を切り落と。すると8個の正三角形が出来る。(3)以上の切り落としで,元の立方体の6つの正方形がそのまま,大きさだけ小さくなって残る。(4)実際には,後に残る18個の正方形と8個の正三角形の辺の長さが同じになる必要があるので,簡単に切り落としてもきちんとした図形は得られない。18個の正方形と,8個の正三角形の合わせて26個の面がある。頂点の形状(3,4,4,4)
⑥大菱形立方八面体:作り方は次のようにイメージできる。(1)まず立方体の12本の辺を削ぎ落とす。つまり面取りする。この場所が次の(2)の段階で12個の正方形になるのである。(2)元の立方体の8個の頂点があった場所を切り落として、8個の正六角形を作る。(3)以上の切り落としで、元の立方体の6つの正方形の場所に6個の正八角形が残ることになる。(4)実際には、後に残る12個の正方形と8個の正六角形、6個の正八角形の辺の長さが同じになる必要があるので、簡単に切り落としてもきちんとした図形は得られない。頂点の形状(4,6,8)
⑦捩れ立方体:作り方は次のようにイメージで出来る。(1)まず立方体の6つの正方形を外側に引っ張り、6つの立方体をそれぞれの中心の周りにまわしてやる。ねじれた6つの正方形の間に隙間ができる。(2)正方形の頂点を適当に3個ずつ選んで結び正三角形を作っていく。6個の正方形と、32個の正三角形の合わせて38個の面がある。頂点の形状(3,3,3,3,4)
⑧小菱形二十面十二面体:構成は比較的容易である。正十二面体から始め,まず正十二面体の辺をすべてそぎ落とし、正十二面体の20個の頂点の位置に正三角形を、そして30本の辺の位置に正方形が出来るように調整する。実際は正十二面体の辺の1/3の長さの位置で辺をそぎ落とせば出来る。30個の正方形と、20個の正三角形、12個の正五角形の合わせて62個の面で出来ている。面の個数は大菱形二十面十二面体と同じ。頂点の形状(3,4,5,4)
⑨大菱形二十面十二面体:構成は二十面十二面体の30個の頂点を切り取ったような形であるが、切り取った辺りには長方形しか出来ないのでこの方法では30個の正方形が出来ない。正方形を作るには,正十二面体から始め,まず正十二面体の辺をすべてそぎ落とす。次に元の正十二面体の頂点周りを切り落とす。辺をそぎ落としたり,頂点周りを切り落とす幅を調節して正方形、正六角形、正十角形を作るのである。30個の正方形と、20個の正六角形、12個の正十角形の合わせて62個の面で出来ている。頂点の形状(4,6,10)
⑩切頂二十面体:構成は他の切頂四面体や切頂立方体、切頂十二面体などと同様に頂点を切り落とすだけなのでイメージしやすい。正二十面体の12個の頂点を切り落とした形に鳴っている。20個の正六角形と、12個の正五角形の合わせて32個の面でできている。頂点の形状は(5,6,6)
⑪切頂十二面体:構成は他の切頂四面体や切頂立方体などと同様に頂点を切り落とすだけなのでイメージしやすい。正十二面体の20個の頂点を切り落とした形になっている。12個の正十角形と,20個の正三角形の合わせて32個の面でできている。頂点の形状(3,10,10)
⑫二十面十二面体:構成は切頂十二面体や切頂二十面体と似ている。まず正十二面体のそれぞれの辺の中点を結んで正三角形を20個作れば出来る。または正二十面体のそれぞれの辺の中点を結んでできた正五角形で頂点を切っていけば出来上がる。20個の正三角形と,12個の正五角形の合わせて32個の面で出来ている。頂点の形状(3,5,3,5)
⑬捩れ十二面体:正十二面体から始め、先ず正十二面体の各面を縮小して辺が約0.56倍になるようにする。次にそれぞれの正五角形をその中心の回りに約13°回転してやる。出来上がった正五角形の頂点を正三角形ができるように結べば出来上がる。
プロフィール
ハンドルネーム:
目高 拙痴无
年齢:
93
誕生日:
1932/02/04
自己紹介:
くたばりかけの糞爺々です。よろしく。メールも頼むね。
sechin@nethome.ne.jp です。
sechin@nethome.ne.jp です。
カレンダー
| 12 | 2026/01 | 02 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
最新コメント
[enken 02/23]
[中村東樹 02/04]
[m、m 02/04]
[爺の姪 01/13]
[レンマ学(メタ数学) 01/02]
[m.m 10/12]
[爺の姪 10/01]
[あは♡ 09/20]
[Mr.サタン 09/20]
[Mr.サタン 09/20]
最新トラックバック
ブログ内検索
カウンター
