瘋癲爺 拙痴无の戯言・放言・歯軋り
Bhāskara2世の数学への貢献には、以下のようなものがある。
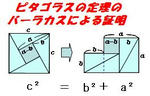 ・ ピタゴラスの定理の証明。同じ領域の面積を2種類の方法で計算し、項を相殺させて消すことで
・ ピタゴラスの定理の証明。同じ領域の面積を2種類の方法で計算し、項を相殺させて消すことで
a² + b² = c² という式を導いた。 (左図参照)
・ 『Lilāvati(リーラーヴァティ)』において、二次方程式、三次方程式、四次方程式の解を示した。
・ 線形および二次の方程式で整数解を求める方法(クッタカ法)。17世紀ルネサンス期のヨーロッパの数学者と同じ方法である。
・ ax²+bx+c=y という形式の方程式を解くChakravala(チャクラバーラ)法 。この方程式は1657年にWilliam Brouncker〔ウィリアム・ブラウンカー、1620?~1684年、イングランド人数学者、医師〕が解いたとされていたが、彼の方法はChakravala(チャクラバーラ)法よりも複雑だった。
・ ペル方程式と呼ばれるx²− ny²=1 という形式の方程式の整数解を求める方法を示した。
・ 61x² + 1 = y² のような二次のディオファントス方程式の解法。この方程式は1657年、フランスの数学者Pierre de Fermat〔ピエール・ド・フェルマー、1607年末または1608年初頭~1665年、フランスの数学者。「数論の父」とも呼ばれる。ただし、職業は弁護士であり、数学は余暇に行ったものであるという〕が問題として提示したが、ヨーロッパでこの解法を明らかにしたのはLeonhard Euler〔レオンハルト・オイラー, 1707~1783年、数学者・物理学者であり、天文学者(天体物理学者)〕で18世紀になってからのことである。
・ 変数が複数ある二次方程式を解き、負数と無理数の解を発見した。
・ 解析学の基本概念。
・ 微分法の基本概念と積分法の元となる貢献。導関数と微分係数を発見。平均値の定理の特殊な場合であるロルの定理を発見。平均値の定理と思われる記述も著作の中に見つかっている。
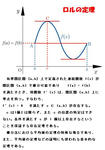 ※ ロルの定理(Rolle's theorem、左図参照) は1691年にフランスの数学者Michel Rolle (ミシェル・ロル、1652~1719年)が著書の「代数学」(Traite d'algebre) で発表されたためにロルの名がついているが、Isaac Newton〔アイザック ニュートン、1642~1727年〕やGottfried Leibniz〔ゴットフリート ライプニッツ、 1646~1716年〕によって微分が発見されるより前の12世紀にインドの天文学者バスカラが同様の定理を述べたとされる。
※ ロルの定理(Rolle's theorem、左図参照) は1691年にフランスの数学者Michel Rolle (ミシェル・ロル、1652~1719年)が著書の「代数学」(Traite d'algebre) で発表されたためにロルの名がついているが、Isaac Newton〔アイザック ニュートン、1642~1727年〕やGottfried Leibniz〔ゴットフリート ライプニッツ、 1646~1716年〕によって微分が発見されるより前の12世紀にインドの天文学者バスカラが同様の定理を述べたとされる。
・ 三角関数の導関数を計算。
・ 『Siddhānta Shiromani(シッダーンタ・シロマーニ)』の中で、いくつかの三角法と共に球面三角法を展開している。
Bhāskara(バースカラ)2世の算術についての著書『Lilāvati(リーラーヴァティ)』は、定義、算術用語、利子計算、算術級数と幾何級数、平面幾何学、立体幾何学、日時計の影、不変方程式の解法、組合せなどを扱っている。
『Lilāvati(リーラーヴァティ)』は13章からなり、算術だけでなく代数学や幾何学も扱い、一部は三角法や求積法を扱っている。具体的には、次のような内容がある。
・ 定義
・ ゼロの性質(除法を含むゼロの演算規則)
・ その他の数に関すること。負数や無理数(冪根)を含む。
・ 円周率の近似値。
・ 算術。乗法や平方など。
・ 利子計算に関する問題。
・ 算術級数と幾何級数。
・ 平面の幾何学。
・ 立体の幾何学。
・ 組合せ数学(順列と組合せ)。
・ 線型および二次の不定方程式の整数解の求め方(クッタカ)。これについては、17世紀ルネサンス期のヨーロッパの数学者と同じ解法を示しており、非常に重要である。バースカラ2世の解法は、アリヤバータなど先人の成果に基づくものだった。
彼の著書は体系化、解法の改善、新たな問題の導入などの点が優れている。さらに『Lilāvati(リーラーヴァティ)』には素晴らしい例題もあり、バースカラ2世は『Lilāvati(リーラーヴァティ)』で学ぶ学生にその内容を具体的に役立てて欲しいと意図していたとも思われる。
『Bijaganita(ビージャガニタ)』(代数学)は12章からなる。正の数に(正と負の)2つの平方根があることを初めて示した文書である。次のような内容を含む。
・正数と負数、 ・ゼロ、 ・未知数、 ・未知の数量の決定、 ・冪根と無理数、
・クッタカ法(不定方程式およびディオファントス方程式の解法)、 ・単純な方程式(二次、三次、四次)
・複数の変数のある単純な方程式、 ・不定二次方程式〔ax² + b = y² という形式のもの〕
・二次、三次、四次の不定方程式の解法、 ・二次方程式、 ・複数の変数のある二次方程式
・複数の変数の積の操作
Bhāskara(バースカラ)2世は ax² + bx + c = y という形式の不定二次方程式の解法としてChakravala(チャクラバーラ)法を導き出した。ペル方程式と呼ばれる Nx² + 1 = y² という形式の問題の整数解を求めるBhāskara(バースカラ)2世の方法も重要である(こちらもChakravala法)という。
 『Siddhānta Shiromani(シッダーンタ・シロマーニ)』〔1150年〕では、三角法を扱っており、正弦関数の数表や各種三角関数の関係も記している。また、いくつかの興味深い三角法に混じって球面三角法も発見している。Bhāskara(バースカラ)2世以前のインドの数学者は三角法を計算の道具としか見ていなかったが、Bhāskara2世自身は三角法に大きな興味を持っていたように思われる。三角関数の加法定理〔左図参照〕といわれる sin(α+β) や sin(α- β) なども扱っている。
『Siddhānta Shiromani(シッダーンタ・シロマーニ)』〔1150年〕では、三角法を扱っており、正弦関数の数表や各種三角関数の関係も記している。また、いくつかの興味深い三角法に混じって球面三角法も発見している。Bhāskara(バースカラ)2世以前のインドの数学者は三角法を計算の道具としか見ていなかったが、Bhāskara2世自身は三角法に大きな興味を持っていたように思われる。三角関数の加法定理〔左図参照〕といわれる sin(α+β) や sin(α- β) なども扱っている。
a² + b² = c² という式を導いた。 (左図参照)
・ 『Lilāvati(リーラーヴァティ)』において、二次方程式、三次方程式、四次方程式の解を示した。
・ 線形および二次の方程式で整数解を求める方法(クッタカ法)。17世紀ルネサンス期のヨーロッパの数学者と同じ方法である。
・ ax²+bx+c=y という形式の方程式を解くChakravala(チャクラバーラ)法 。この方程式は1657年にWilliam Brouncker〔ウィリアム・ブラウンカー、1620?~1684年、イングランド人数学者、医師〕が解いたとされていたが、彼の方法はChakravala(チャクラバーラ)法よりも複雑だった。
・ ペル方程式と呼ばれるx²− ny²=1 という形式の方程式の整数解を求める方法を示した。
・ 61x² + 1 = y² のような二次のディオファントス方程式の解法。この方程式は1657年、フランスの数学者Pierre de Fermat〔ピエール・ド・フェルマー、1607年末または1608年初頭~1665年、フランスの数学者。「数論の父」とも呼ばれる。ただし、職業は弁護士であり、数学は余暇に行ったものであるという〕が問題として提示したが、ヨーロッパでこの解法を明らかにしたのはLeonhard Euler〔レオンハルト・オイラー, 1707~1783年、数学者・物理学者であり、天文学者(天体物理学者)〕で18世紀になってからのことである。
・ 変数が複数ある二次方程式を解き、負数と無理数の解を発見した。
・ 解析学の基本概念。
・ 微分法の基本概念と積分法の元となる貢献。導関数と微分係数を発見。平均値の定理の特殊な場合であるロルの定理を発見。平均値の定理と思われる記述も著作の中に見つかっている。
・ 三角関数の導関数を計算。
・ 『Siddhānta Shiromani(シッダーンタ・シロマーニ)』の中で、いくつかの三角法と共に球面三角法を展開している。
Bhāskara(バースカラ)2世の算術についての著書『Lilāvati(リーラーヴァティ)』は、定義、算術用語、利子計算、算術級数と幾何級数、平面幾何学、立体幾何学、日時計の影、不変方程式の解法、組合せなどを扱っている。
『Lilāvati(リーラーヴァティ)』は13章からなり、算術だけでなく代数学や幾何学も扱い、一部は三角法や求積法を扱っている。具体的には、次のような内容がある。
・ 定義
・ ゼロの性質(除法を含むゼロの演算規則)
・ その他の数に関すること。負数や無理数(冪根)を含む。
・ 円周率の近似値。
・ 算術。乗法や平方など。
・ 利子計算に関する問題。
・ 算術級数と幾何級数。
・ 平面の幾何学。
・ 立体の幾何学。
・ 組合せ数学(順列と組合せ)。
・ 線型および二次の不定方程式の整数解の求め方(クッタカ)。これについては、17世紀ルネサンス期のヨーロッパの数学者と同じ解法を示しており、非常に重要である。バースカラ2世の解法は、アリヤバータなど先人の成果に基づくものだった。
彼の著書は体系化、解法の改善、新たな問題の導入などの点が優れている。さらに『Lilāvati(リーラーヴァティ)』には素晴らしい例題もあり、バースカラ2世は『Lilāvati(リーラーヴァティ)』で学ぶ学生にその内容を具体的に役立てて欲しいと意図していたとも思われる。
『Bijaganita(ビージャガニタ)』(代数学)は12章からなる。正の数に(正と負の)2つの平方根があることを初めて示した文書である。次のような内容を含む。
・正数と負数、 ・ゼロ、 ・未知数、 ・未知の数量の決定、 ・冪根と無理数、
・クッタカ法(不定方程式およびディオファントス方程式の解法)、 ・単純な方程式(二次、三次、四次)
・複数の変数のある単純な方程式、 ・不定二次方程式〔ax² + b = y² という形式のもの〕
・二次、三次、四次の不定方程式の解法、 ・二次方程式、 ・複数の変数のある二次方程式
・複数の変数の積の操作
Bhāskara(バースカラ)2世は ax² + bx + c = y という形式の不定二次方程式の解法としてChakravala(チャクラバーラ)法を導き出した。ペル方程式と呼ばれる Nx² + 1 = y² という形式の問題の整数解を求めるBhāskara(バースカラ)2世の方法も重要である(こちらもChakravala法)という。
PR
この記事にコメントする
プロフィール
ハンドルネーム:
目高 拙痴无
年齢:
93
誕生日:
1932/02/04
自己紹介:
くたばりかけの糞爺々です。よろしく。メールも頼むね。
sechin@nethome.ne.jp です。
sechin@nethome.ne.jp です。
カレンダー
| 11 | 2025/12 | 01 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
最新コメント
[enken 02/23]
[中村東樹 02/04]
[m、m 02/04]
[爺の姪 01/13]
[レンマ学(メタ数学) 01/02]
[m.m 10/12]
[爺の姪 10/01]
[あは♡ 09/20]
[Mr.サタン 09/20]
[Mr.サタン 09/20]
最新トラックバック
ブログ内検索
カウンター
