瘋癲爺 拙痴无の戯言・放言・歯軋り
「無」を表す「0」を数の対象として考える概念の発生は、数学上の飛躍的な進歩の過程の一つと考えられている。
バビロニアとマヤ文明では、位取り記数法で空位を示す記号としての 0 が使われていた。バビロニアを含むメソポタミア文明は六十進法、マヤは二十進法を用いており、それぞれで位が 0 であることを示す独自の記号が発明された。しかし 0 そのものを数として扱ってはいなかった。
一方、古代エジプトでは0 の存在を知っていたが発達せず、それを表す記号もなかった。0 を四則演算などで扱うと矛盾が生ずるので、無理数同様、受け入れられなかった。
130年、Claudius Ptolemaeus〔クラウディオス プトレマイオス, 83?~168年頃)がギリシア文字を用いた六十進法の表記において、0 を導入したのが、記録に残っている最も古い、数としての0 である。ただしPtolemaeus(プトレマイオス)が 0 を用いたのは分数部分(分、秒など)だけであり、整数部分(度)には使わなかったという。
その後、インドの数学で「膨れ上がった」「うつろな」の意サンスクリット語では śūnya (シューニャ 膨れ上がった物は中が空であるとの考え方から来ている。)すなわち数としての0 の概念が確立された。Brahmagupta〔ブラーマグプタ、598~668?年〕は、628年に著した『Brahmasphutasiddhanta(ブラーマ・スプタ・シッダーンタ)』において、0と他の整数との加減乗除を論じ、0/0 を 0 と定義した以外はすべて現代と同じ定義をしている。そしてこれがアラビア数学に伝わりal―Khwārizmī〔アル=フワーリズミー、780?~850?年〕の著作の Algoritmi de numero Indorum〔アルゴリトミ・デ・ヌーメロ・インドルム、直訳すると「インドの数に関して」、ラテン語訳〕により西欧に広まっていった。
中国では算木が紀元前から使われており、位取り記数法が確立していたが、空位は空白で表していた。算木を実際に使うときは誤解がないが、それを書写するときは紛らわしい。後に空位を「〇」と書くようになった。これはインドの(0)が輸入されたとも、元々、漢文で空白を表す「囗」が「〇」に変化したともいう。
仏教ではシューニャ(漢訳で空)は真に実在するものではなく、その真相は空虚であると説いている。
※ 空とは、仏教の因果論の究極形であり、因果および因縁の複雑な連関である(したがって、空を理解するにはまず因果および因縁を理解する必要がある)。この世のすべての物事(色)は相互に因縁によって結びつき、ある現象を構成している。この因縁の関係性こそが「空」だという考えである。例えば、そこらの草木を建材として庵を結ぶ場合、庵は草木から作られ、さらに草木も微細に分解していくことができ、どこにも庵という現象は成立していないことになる。つまり、庵は「存在している」とも言えず、「存在していない」とも言えない。このような「有る」と「無い」の二つの極端を離れたあり方を空という。
数の 0 は最小の非負整数である。0の後続の自然数は 1 であり、0 より前に自然数は存在しない。数 0 を自然数に含めることも含めないこともあるが、0は整数であり、有理数であり、実数(あるいは代数的数、複素数)である。
数 0 は正でも負でもなく、素数でも合成数でも単数でもない。しかし、0は偶数である。
以下は数 0 を扱う上での初等的な決まりごとである。これらの決まりはx を任意の実数あるいは複素数として適用して構わないが、それ以外の場合については何も言及していないということについては理解されなければならない。
加法: x + 0 =0 + x = x. つまり 0 は加法に関する中立元である。
減法: x − 0 = x and 0 − x= −x.
乗法: ⅹ · 0 = 0 · x = 0.
 除法: x が 0 でなければ0/ⅹ = 0 である。しかし x/0 は、0 が乗法に関する逆元を持たないために、(従前の規則の帰結としては)定義されない。実数の範囲で考えるならば、正の数x に対し、商 x/y の y を 0 に正の側から近づけるならば、商の値は正の無限大に向かって無限に増加する。一方 y を負の側から 0 に近づければ、商の値は負の値に近づく。言い換えれば、左図のように表すことが出来る。
除法: x が 0 でなければ0/ⅹ = 0 である。しかし x/0 は、0 が乗法に関する逆元を持たないために、(従前の規則の帰結としては)定義されない。実数の範囲で考えるならば、正の数x に対し、商 x/y の y を 0 に正の側から近づけるならば、商の値は正の無限大に向かって無限に増加する。一方 y を負の側から 0 に近づければ、商の値は負の値に近づく。言い換えれば、左図のように表すことが出来る。
冪乗: x = 0の場合にきちんと定義できないまま残される文脈があることを除けば、
ⅹ⁰ = ⅹ/ⅹ = 1 である。任意の正の実数 x に対して0x = 0 である。
 0/0 なる式が、f(x)/g(x) の形の式の極限を決定しようとするなかで、それぞれ独立に分子分母の極限を取った結果として現れるかもしれない。これは不定形と呼ばれる。これは単に必ずしも極限が求まらないということを意味するものではなく、むしろf(x)/g(x) の極限は、それが存在するならば、ロピタルの定理(左図参照)のような別の方法によって求めるべきであるということを意味する。
0/0 なる式が、f(x)/g(x) の形の式の極限を決定しようとするなかで、それぞれ独立に分子分母の極限を取った結果として現れるかもしれない。これは不定形と呼ばれる。これは単に必ずしも極限が求まらないということを意味するものではなく、むしろf(x)/g(x) の極限は、それが存在するならば、ロピタルの定理(左図参照)のような別の方法によって求めるべきであるということを意味する。
※ ロピタル侯爵Guillaume Francois Antoine〔ギヨーム・フランソワ・アントワーヌ、1661~1704年〕は、フランスの数学者。微分積分学における平均値の定理の別名、ロピタルの定理にその名を残しているが、当の定理はロピタルの発見によるものではない。ロピタルという名前は一般的に l'Hospital または l'Hôpital と綴られる。
0 個の対象の和は0 であり、 0 個の対象の積は 1 である。階乗 0! は 1 と評価される。
バビロニアとマヤ文明では、位取り記数法で空位を示す記号としての 0 が使われていた。バビロニアを含むメソポタミア文明は六十進法、マヤは二十進法を用いており、それぞれで位が 0 であることを示す独自の記号が発明された。しかし 0 そのものを数として扱ってはいなかった。
一方、古代エジプトでは0 の存在を知っていたが発達せず、それを表す記号もなかった。0 を四則演算などで扱うと矛盾が生ずるので、無理数同様、受け入れられなかった。
130年、Claudius Ptolemaeus〔クラウディオス プトレマイオス, 83?~168年頃)がギリシア文字を用いた六十進法の表記において、0 を導入したのが、記録に残っている最も古い、数としての0 である。ただしPtolemaeus(プトレマイオス)が 0 を用いたのは分数部分(分、秒など)だけであり、整数部分(度)には使わなかったという。
その後、インドの数学で「膨れ上がった」「うつろな」の意サンスクリット語では śūnya (シューニャ 膨れ上がった物は中が空であるとの考え方から来ている。)すなわち数としての0 の概念が確立された。Brahmagupta〔ブラーマグプタ、598~668?年〕は、628年に著した『Brahmasphutasiddhanta(ブラーマ・スプタ・シッダーンタ)』において、0と他の整数との加減乗除を論じ、0/0 を 0 と定義した以外はすべて現代と同じ定義をしている。そしてこれがアラビア数学に伝わりal―Khwārizmī〔アル=フワーリズミー、780?~850?年〕の著作の Algoritmi de numero Indorum〔アルゴリトミ・デ・ヌーメロ・インドルム、直訳すると「インドの数に関して」、ラテン語訳〕により西欧に広まっていった。
中国では算木が紀元前から使われており、位取り記数法が確立していたが、空位は空白で表していた。算木を実際に使うときは誤解がないが、それを書写するときは紛らわしい。後に空位を「〇」と書くようになった。これはインドの(0)が輸入されたとも、元々、漢文で空白を表す「囗」が「〇」に変化したともいう。
仏教ではシューニャ(漢訳で空)は真に実在するものではなく、その真相は空虚であると説いている。
※ 空とは、仏教の因果論の究極形であり、因果および因縁の複雑な連関である(したがって、空を理解するにはまず因果および因縁を理解する必要がある)。この世のすべての物事(色)は相互に因縁によって結びつき、ある現象を構成している。この因縁の関係性こそが「空」だという考えである。例えば、そこらの草木を建材として庵を結ぶ場合、庵は草木から作られ、さらに草木も微細に分解していくことができ、どこにも庵という現象は成立していないことになる。つまり、庵は「存在している」とも言えず、「存在していない」とも言えない。このような「有る」と「無い」の二つの極端を離れたあり方を空という。
数の 0 は最小の非負整数である。0の後続の自然数は 1 であり、0 より前に自然数は存在しない。数 0 を自然数に含めることも含めないこともあるが、0は整数であり、有理数であり、実数(あるいは代数的数、複素数)である。
数 0 は正でも負でもなく、素数でも合成数でも単数でもない。しかし、0は偶数である。
以下は数 0 を扱う上での初等的な決まりごとである。これらの決まりはx を任意の実数あるいは複素数として適用して構わないが、それ以外の場合については何も言及していないということについては理解されなければならない。
加法: x + 0 =0 + x = x. つまり 0 は加法に関する中立元である。
減法: x − 0 = x and 0 − x= −x.
乗法: ⅹ · 0 = 0 · x = 0.
冪乗: x = 0の場合にきちんと定義できないまま残される文脈があることを除けば、
ⅹ⁰ = ⅹ/ⅹ = 1 である。任意の正の実数 x に対して0x = 0 である。
※ ロピタル侯爵Guillaume Francois Antoine〔ギヨーム・フランソワ・アントワーヌ、1661~1704年〕は、フランスの数学者。微分積分学における平均値の定理の別名、ロピタルの定理にその名を残しているが、当の定理はロピタルの発見によるものではない。ロピタルという名前は一般的に l'Hospital または l'Hôpital と綴られる。
0 個の対象の和は0 であり、 0 個の対象の積は 1 である。階乗 0! は 1 と評価される。
PR
ご承知の通り、文明は大河のほとりに起こった。そしてそのうち最も有名なのがエジプトのナイル河のほとり、バビロニアのチグリス・ユーフラテス河のほとり、インドのガンジス・インダス河のほとり、そして中国の黄河のほとりであった。
インドに起こった数学は、アラビアを経て、やがてヨーロッパに輸入され、ローマの数学と結びついて、种世の数学を形成して言ったのである。
我々の遠い祖先が、まだ、1、2、3、4、…と数を数えることを知らなかった時代に、そこに幾つかのものがあるかを記憶したり、記録しようとする場合には、そこにあるものと1対1の対応がつく見本を利用していた。たとえば、ある未開人が、自分の家畜の数を記録しておこうとする場合には、その家畜の集まりと1対1の対応が付くような刻み目を木の幹につけていたといわれる。英語に刻み目をいみする tally(タリー) という語があるが、辞書で調べてみると「割符、刻み目、計算、得点、金利、計算単位」などを意味するとあるが、これは人類が数を覚え計算を覚えるのに木の幹につけた刻み目から出発したことのよい証拠であろう。
また、未開人の酋長が自分の部族の数を記録しておくのに、小石を1つずつ部族の人たちに渡して、それをまた集めてしまっておくということをする。この場合彼の部族の人たちの集合と小石の集合には1対1の対応があるわけである。英語に小石を意味するcalculus(カルキュラス)という語があるが、これも辞書をひいてみると、「結石、石、計算、微分積分学」など意味するとあるが、これも人類が数を覚え、計算を覚える最初に小石を利用していた証拠になるであろう。
しかし、このような見本がいつも身近に見付かるとは限らないので、人類はそこにある集合の見本として自分自身の身体を使うことに気づいていったものと思われる。その見本として、我々の手と足についている指が最も適しているものであることを発見したのであろう。こうして、人類は
 1つ、2つ。3つ、4つ、片手、片手と1つ、……
1つ、2つ。3つ、4つ、片手、片手と1つ、……
と数えることを覚えたと思われる。このように、片手でまず1まとまり、次にその1まとまりと1つ、その1まとまりと2つと数えていくとすれば、これはいわゆる5進法である。人類が1度はこの5で1まとまりと考える5進法を使っていた名残りは方々に見出すことが出来る。(左図参照)
しかし、1つ、2つ、3つ、4つ、5つ、6つ、7つ、8つ、9つ、両手、両手と1つ、両手と2つ、……
と両手が終わった時、すなわち10になったとき、それを1まとまりだと考えたとすれば、それは現在われわれが使っている10進法である。
しかし、未開人たちは、両手が終ってもまだ勘定が終わらない場合うには、足の指に移って、
両手と足の指1つ、両手と足の指2つ、……
というように勘定を進めて、両手、両足の指が終わるまで、つまり20まで数えて、それを1まとまりと考えた時期もあったと思われる。
英語では20のことを普通は twenty というが、これは明らかに2(two)という言葉と10(ten)という言葉を合わせて作った言葉である。ところが、1語で20を意味する score という言葉があり、例えば70のことを「three score and ten〔3つの20と10〕」などというのは、昔20を1まとまりと考えていた時代のあることを示す証拠といえる。試みにこの score を辞典でひいてみると、
刻み目、勘定、得点、20、多数
などを意味することが判るが、これは人類が数を覚えていった歴史をあらわすものといえる。最後の〔多数〕というのは、未開人にとって20はもう大きな数であったのであろう。現在でも「沲数回」をいみするものに、「score of times」と言う言い方がある。
 しかし、5では1まとめとして小さ過ぎ、20では1まとめとして大き過ぎるという理由と、両手の指は自由に伸ばしたり折ったりできるという理由からであろう、人間は10進法を採用して今日に到っている。1つの単位が10集まって位が上るたびに新しい記号を用いていた。(左図参照)
しかし、5では1まとめとして小さ過ぎ、20では1まとめとして大き過ぎるという理由と、両手の指は自由に伸ばしたり折ったりできるという理由からであろう、人間は10進法を採用して今日に到っている。1つの単位が10集まって位が上るたびに新しい記号を用いていた。(左図参照)
これに対して、今日用いている記数法においては、
1、2、3、4、5、6、7、8、9と数えていって、その次の10をしめすには、ここにある9つの数字以外にもう1つ「0」という記号を用意しておいて、「10」とする。その次は、
11、12、13、……、20、21、……、90、91、……99、
と進み、10が10まとまった時にも、新しい記号を導入することなく、「100」とする。すなわち、我々は1、2、3、4、5、6、7、8、9 という9つの数字のほかに「0」という記号を用いて、例えば、 2803 のように、たった10個の数字を用いて全ての数を書き表すようになったのである。
このように、0という記号を用い、これを利用して位取り記数法を活用するというこの方法は、インドの人びとの考え出したものであり、このことを普通「0の発見」と呼んでいる。この0の発見こそは、古代インドの人たちが我々に残してくれた最大の遺産というべきであろう。
インドに起こった数学は、アラビアを経て、やがてヨーロッパに輸入され、ローマの数学と結びついて、种世の数学を形成して言ったのである。
我々の遠い祖先が、まだ、1、2、3、4、…と数を数えることを知らなかった時代に、そこに幾つかのものがあるかを記憶したり、記録しようとする場合には、そこにあるものと1対1の対応がつく見本を利用していた。たとえば、ある未開人が、自分の家畜の数を記録しておこうとする場合には、その家畜の集まりと1対1の対応が付くような刻み目を木の幹につけていたといわれる。英語に刻み目をいみする tally(タリー) という語があるが、辞書で調べてみると「割符、刻み目、計算、得点、金利、計算単位」などを意味するとあるが、これは人類が数を覚え計算を覚えるのに木の幹につけた刻み目から出発したことのよい証拠であろう。
また、未開人の酋長が自分の部族の数を記録しておくのに、小石を1つずつ部族の人たちに渡して、それをまた集めてしまっておくということをする。この場合彼の部族の人たちの集合と小石の集合には1対1の対応があるわけである。英語に小石を意味するcalculus(カルキュラス)という語があるが、これも辞書をひいてみると、「結石、石、計算、微分積分学」など意味するとあるが、これも人類が数を覚え、計算を覚える最初に小石を利用していた証拠になるであろう。
しかし、このような見本がいつも身近に見付かるとは限らないので、人類はそこにある集合の見本として自分自身の身体を使うことに気づいていったものと思われる。その見本として、我々の手と足についている指が最も適しているものであることを発見したのであろう。こうして、人類は
と数えることを覚えたと思われる。このように、片手でまず1まとまり、次にその1まとまりと1つ、その1まとまりと2つと数えていくとすれば、これはいわゆる5進法である。人類が1度はこの5で1まとまりと考える5進法を使っていた名残りは方々に見出すことが出来る。(左図参照)
しかし、1つ、2つ、3つ、4つ、5つ、6つ、7つ、8つ、9つ、両手、両手と1つ、両手と2つ、……
と両手が終わった時、すなわち10になったとき、それを1まとまりだと考えたとすれば、それは現在われわれが使っている10進法である。
しかし、未開人たちは、両手が終ってもまだ勘定が終わらない場合うには、足の指に移って、
両手と足の指1つ、両手と足の指2つ、……
というように勘定を進めて、両手、両足の指が終わるまで、つまり20まで数えて、それを1まとまりと考えた時期もあったと思われる。
英語では20のことを普通は twenty というが、これは明らかに2(two)という言葉と10(ten)という言葉を合わせて作った言葉である。ところが、1語で20を意味する score という言葉があり、例えば70のことを「three score and ten〔3つの20と10〕」などというのは、昔20を1まとまりと考えていた時代のあることを示す証拠といえる。試みにこの score を辞典でひいてみると、
刻み目、勘定、得点、20、多数
などを意味することが判るが、これは人類が数を覚えていった歴史をあらわすものといえる。最後の〔多数〕というのは、未開人にとって20はもう大きな数であったのであろう。現在でも「沲数回」をいみするものに、「score of times」と言う言い方がある。
これに対して、今日用いている記数法においては、
1、2、3、4、5、6、7、8、9と数えていって、その次の10をしめすには、ここにある9つの数字以外にもう1つ「0」という記号を用意しておいて、「10」とする。その次は、
11、12、13、……、20、21、……、90、91、……99、
と進み、10が10まとまった時にも、新しい記号を導入することなく、「100」とする。すなわち、我々は1、2、3、4、5、6、7、8、9 という9つの数字のほかに「0」という記号を用いて、例えば、 2803 のように、たった10個の数字を用いて全ての数を書き表すようになったのである。
このように、0という記号を用い、これを利用して位取り記数法を活用するというこの方法は、インドの人びとの考え出したものであり、このことを普通「0の発見」と呼んでいる。この0の発見こそは、古代インドの人たちが我々に残してくれた最大の遺産というべきであろう。
Alexandria(アレキサンドリア)のPappus(パップス)はAlexandria生まれのエジプトの数学者。4世紀の前半に活躍した。
彼はギリシャ数学を幅広く渉猟し、その技法を修得して8巻に及ぶ数学上の著作を残していること以外には、彼の生涯については、あまりよく知られていない。しかし、彼はその第七巻において、パップス=ギュルダンの定理と呼ばれる定理を証明しているが、これは後世の数学者に大きな影響を与えた。その他、三角形の中線定理(パップスの定理)など平面幾何学のいくつかの定理に彼の名前が残っている。
 ※ Pappus-Guldin(パップス・ギュルダン)の定理は、回転体の体積に関する定理である。AlexandriaアレキサンドリアのPappus(パップス)によって発見され、後にPaul Guldin〔パウル・ギュルダン、1577~1643年、スイス生まれのオーストリアの数学者〕によって独立に発見された。(左図参照)
※ Pappus-Guldin(パップス・ギュルダン)の定理は、回転体の体積に関する定理である。AlexandriaアレキサンドリアのPappus(パップス)によって発見され、後にPaul Guldin〔パウル・ギュルダン、1577~1643年、スイス生まれのオーストリアの数学者〕によって独立に発見された。(左図参照)
 ※ 中線定理(ちゅうせんていり)とは、幾何学において、三角形の中線の長さと辺の長さの関係を表す定理である。Pappus(パップス)の定理ともいわれる。(左図参照)
※ 中線定理(ちゅうせんていり)とは、幾何学において、三角形の中線の長さと辺の長さの関係を表す定理である。Pappus(パップス)の定理ともいわれる。(左図参照)
彼はギリシャ数学を幅広く渉猟し、その技法を修得して8巻に及ぶ数学上の著作を残していること以外には、彼の生涯については、あまりよく知られていない。しかし、彼はその第七巻において、パップス=ギュルダンの定理と呼ばれる定理を証明しているが、これは後世の数学者に大きな影響を与えた。その他、三角形の中線定理(パップスの定理)など平面幾何学のいくつかの定理に彼の名前が残っている。
前回の衆院選には出馬せず、この6月一杯で、民主党からも離党すると聞いていた鳩山由紀夫元首相、大人しくなりを潜めているものと思っていたが、なにやらかつての妄言癖は治ってないらしく、またまた迷発言で世間を騒がしているらしい。ウェブニュースより
 鳩山氏“売国発言”に識者ら激怒!「許しがたい」「頭がお花畑に…」 ―― 鳩山由紀夫元首相が、信じられない売国発言を炸裂させた。香港のフェニックステレビの取材に対し、沖縄県・尖閣諸島の領有権を主張する中国政府に理解を示したうえで、「中国側から『日本が(尖閣を)盗んだ』と思われても仕方がない」と述べたのだ。中国による尖閣強奪謀略に加担するような言動に、民主党時代の同志や、沖縄県の地元関係者、識者らは怒り心頭に発している。/衝撃発言は25日午前、中国内外に向けて報道された。
鳩山氏“売国発言”に識者ら激怒!「許しがたい」「頭がお花畑に…」 ―― 鳩山由紀夫元首相が、信じられない売国発言を炸裂させた。香港のフェニックステレビの取材に対し、沖縄県・尖閣諸島の領有権を主張する中国政府に理解を示したうえで、「中国側から『日本が(尖閣を)盗んだ』と思われても仕方がない」と述べたのだ。中国による尖閣強奪謀略に加担するような言動に、民主党時代の同志や、沖縄県の地元関係者、識者らは怒り心頭に発している。/衝撃発言は25日午前、中国内外に向けて報道された。
 鳩山氏は「日本が盗んだ~」との発言に加え、「『私の島だ』という気持ちを(日中)両方の国が持つのは当然だ」とも述べ、日本が領有権問題の存在を認めるべきとの認識まで強調した。/すでに政界を離れている鳩山氏だが、首相経験者の言動だけに、日中両国の世論に影響を与える可能性や、中国に悪用される危険性もある。
鳩山氏は「日本が盗んだ~」との発言に加え、「『私の島だ』という気持ちを(日中)両方の国が持つのは当然だ」とも述べ、日本が領有権問題の存在を認めるべきとの認識まで強調した。/すでに政界を離れている鳩山氏だが、首相経験者の言動だけに、日中両国の世論に影響を与える可能性や、中国に悪用される危険性もある。
 民主党の石井一副代表は「軽率極まる発言だ。彼を首相に擁立した1人として、恥ずかしさを禁じ得ない」といい、こう怒りをぶつけた。/「本人は軽い気持ちで言ったのだろうが、国益を害しかねない問題だ。政治家は公人であり、辞めても発言に責任を持たなくては。過去にもいろんな失言があったが、そもそも、黙っていればいいのだ。中国が尖閣の領有権を主張し始めたのは、国連調査で周辺に石油が埋蔵されていると発表されてから。米国もそれ以外の国も、民主党議員の多くも『尖閣は日本領土だ』と分かっている」
民主党の石井一副代表は「軽率極まる発言だ。彼を首相に擁立した1人として、恥ずかしさを禁じ得ない」といい、こう怒りをぶつけた。/「本人は軽い気持ちで言ったのだろうが、国益を害しかねない問題だ。政治家は公人であり、辞めても発言に責任を持たなくては。過去にもいろんな失言があったが、そもそも、黙っていればいいのだ。中国が尖閣の領有権を主張し始めたのは、国連調査で周辺に石油が埋蔵されていると発表されてから。米国もそれ以外の国も、民主党議員の多くも『尖閣は日本領土だ』と分かっている」
 尖閣の地元・沖縄県石垣市にも鳩山発言は伝わった。同市を拠点にする地方紙「八重山日報」の仲新城誠編集長は「考えられない。許しがたい」といい、こう語った。/「現在、石垣島の漁師は、中国公船が尖閣周辺に連日侵入してくるため、漁ができない状況に追い込まれている。国に対して『実効支配を強めてほしい』と要望している。こうしたなかで、元首相がこういう発言をするとは許せない。民主党は2010年の尖閣沖中国漁船衝突事件で弱腰に終始し、地元を失望させた。鳩山氏がまだ党員ならば、海江田万里代表は除名するなど、毅然とした姿勢を見せてほしい」
尖閣の地元・沖縄県石垣市にも鳩山発言は伝わった。同市を拠点にする地方紙「八重山日報」の仲新城誠編集長は「考えられない。許しがたい」といい、こう語った。/「現在、石垣島の漁師は、中国公船が尖閣周辺に連日侵入してくるため、漁ができない状況に追い込まれている。国に対して『実効支配を強めてほしい』と要望している。こうしたなかで、元首相がこういう発言をするとは許せない。民主党は2010年の尖閣沖中国漁船衝突事件で弱腰に終始し、地元を失望させた。鳩山氏がまだ党員ならば、海江田万里代表は除名するなど、毅然とした姿勢を見せてほしい」
 中国側の狡猾な仕掛けと、鳩山氏の愚鈍ぶりを指摘する声もある。/ノンフィクション作家の河添恵子氏は「あきれ果てる。私は、首相時代の鳩山氏を『ハトがサギになった』と評したが、ついに『頭がお花畑になった』ようだ」といい、こう続けた。/「鳩山氏は、米国には『トラスト・ミー』で見捨てられ、祖父・一郎氏が近かったロシアにも相手にされず、残された大国・中国の誘いに乗ったのだろう。ゆがんだ自己顕示欲といえる。中国側としては『日本国元首相』というブランドを利用して、自分たちに都合のいい宣伝工作をしている。このまま放置すれば、どんどん国益を害する。国会で元首相の肩書を剥奪するとかできないものか。弟で自民党の鳩山邦夫元総務相に『鳩山一族の責任』で、何とかしてほしい」 〔ZAKZAK 2013.06.26〕
中国側の狡猾な仕掛けと、鳩山氏の愚鈍ぶりを指摘する声もある。/ノンフィクション作家の河添恵子氏は「あきれ果てる。私は、首相時代の鳩山氏を『ハトがサギになった』と評したが、ついに『頭がお花畑になった』ようだ」といい、こう続けた。/「鳩山氏は、米国には『トラスト・ミー』で見捨てられ、祖父・一郎氏が近かったロシアにも相手にされず、残された大国・中国の誘いに乗ったのだろう。ゆがんだ自己顕示欲といえる。中国側としては『日本国元首相』というブランドを利用して、自分たちに都合のいい宣伝工作をしている。このまま放置すれば、どんどん国益を害する。国会で元首相の肩書を剥奪するとかできないものか。弟で自民党の鳩山邦夫元総務相に『鳩山一族の責任』で、何とかしてほしい」 〔ZAKZAK 2013.06.26〕
昨日の朝刊によれば、現在でもフランスでは最もよく知られた日本人画家である藤田嗣治の晩年の作であるが、未発表の作品が初公開されるという。
ウェブニュースに拠る記事に曰く、



藤田嗣治の未発表作 世界初公開へ ―― 独特の乳白色を基調とした裸婦像などで知られ、国内外で人気を集めた画家、藤田嗣治が晩年に描いた未発表の油絵2点が、7月、神奈川県の美術館で、世界で初めて公開されることになりました。/藤田嗣治は、明治19年に東京で生まれ、大正2年にフランスに渡って、独特の乳白色を基調とした裸婦像などで高く評価され、戦後はフランス国籍を取得し、昭和43年、81歳で亡くなりました。藤田の作品は遺族が長年保管していましたが、このほど、晩年に描かれた未発表の油絵2点を、個人のコレクターが購入していたことが分かりました。/このうち、1952(昭和27)年に描かれた作品「シレーヌ」は、ギリシャ神話に登場する人魚、「セイレーン」を題材に、女性や子どもの人魚を独特の色彩で描いています。/また、1955(昭和30)年に描かれた「グロテスク」という作品は、上半身裸で横たわる女性の周りに、さまざまな不自然な形の顔が描かれた幻想的な絵です。/作品を調べたポーラ美術館の学芸員、内呂博之さんは、「藤田は晩年にキリスト教の洗礼を受けているが、新たに公開される絵画にはキリスト教的な要素もうかがわれる。/これまで発表された作品にはない表現があり、晩年の藤田の芸術の本質に迫る貴重な作品だ」と話しています。/これらの作品は、7月13日から、神奈川県箱根町のポーラ美術館で初めて公開されます。 〔NHK NEWS WEB 6月24日 14時46分〕
今朝の朝刊に拠れば、今年の夏も猛暑になるらしい。以下、朝日新聞社会面に曰く、
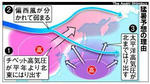 7~9月は猛暑・少雨、北海道から九州まで 気象庁予報 ―― 気象庁は25日、北海道から九州までの広い範囲で7~9月は猛暑になるとの3カ月予報を発表した。太平洋高気圧が北に張り出して列島を広く覆い、晴れの日が多くなるからだという。一方、沖縄・奄美は高気圧の外側になり、雨の日が多くなると予想した。/予報によると、中国大陸にあるチベット高気圧の勢力が平年と比べて強く、7月以降は北東に張り出してくる。偏西風がチベット高気圧に押されて一部が北に分かれるため、日本付近での流れが弱まる。偏西風の南に位置する太平洋高気圧が平年より北に張り出しやすくなる。その結果、列島の広い範囲で晴れの日が増え、気温が上がるという。/この傾向が最も顕著になるのは8月で、各地で猛暑日(35度以上)が続く見込みだ。半面、太平洋高気圧の縁に当たる沖縄・奄美地方は湿った暖気の通り道になって雨が降りやすく、気温も平年並みにとどまるという。
7~9月は猛暑・少雨、北海道から九州まで 気象庁予報 ―― 気象庁は25日、北海道から九州までの広い範囲で7~9月は猛暑になるとの3カ月予報を発表した。太平洋高気圧が北に張り出して列島を広く覆い、晴れの日が多くなるからだという。一方、沖縄・奄美は高気圧の外側になり、雨の日が多くなると予想した。/予報によると、中国大陸にあるチベット高気圧の勢力が平年と比べて強く、7月以降は北東に張り出してくる。偏西風がチベット高気圧に押されて一部が北に分かれるため、日本付近での流れが弱まる。偏西風の南に位置する太平洋高気圧が平年より北に張り出しやすくなる。その結果、列島の広い範囲で晴れの日が増え、気温が上がるという。/この傾向が最も顕著になるのは8月で、各地で猛暑日(35度以上)が続く見込みだ。半面、太平洋高気圧の縁に当たる沖縄・奄美地方は湿った暖気の通り道になって雨が降りやすく、気温も平年並みにとどまるという。
ウェブニュースに拠る記事に曰く、
藤田嗣治の未発表作 世界初公開へ ―― 独特の乳白色を基調とした裸婦像などで知られ、国内外で人気を集めた画家、藤田嗣治が晩年に描いた未発表の油絵2点が、7月、神奈川県の美術館で、世界で初めて公開されることになりました。/藤田嗣治は、明治19年に東京で生まれ、大正2年にフランスに渡って、独特の乳白色を基調とした裸婦像などで高く評価され、戦後はフランス国籍を取得し、昭和43年、81歳で亡くなりました。藤田の作品は遺族が長年保管していましたが、このほど、晩年に描かれた未発表の油絵2点を、個人のコレクターが購入していたことが分かりました。/このうち、1952(昭和27)年に描かれた作品「シレーヌ」は、ギリシャ神話に登場する人魚、「セイレーン」を題材に、女性や子どもの人魚を独特の色彩で描いています。/また、1955(昭和30)年に描かれた「グロテスク」という作品は、上半身裸で横たわる女性の周りに、さまざまな不自然な形の顔が描かれた幻想的な絵です。/作品を調べたポーラ美術館の学芸員、内呂博之さんは、「藤田は晩年にキリスト教の洗礼を受けているが、新たに公開される絵画にはキリスト教的な要素もうかがわれる。/これまで発表された作品にはない表現があり、晩年の藤田の芸術の本質に迫る貴重な作品だ」と話しています。/これらの作品は、7月13日から、神奈川県箱根町のポーラ美術館で初めて公開されます。 〔NHK NEWS WEB 6月24日 14時46分〕
今朝の朝刊に拠れば、今年の夏も猛暑になるらしい。以下、朝日新聞社会面に曰く、
エジプトのAlexandria(アレキサンドリア)に住んでいたということ以外は、彼の人生についての詳細は不明。ディオファントスの著した13巻に及ぶ『算術』 ("Arithmetica(アリスメティカ)") が有名である。同書が翻訳された16世紀以降のヨーロッパにおける代数学発展に深く影響した。(現存している同書のギリシャ語版は6巻分のみ、アラビア語版は4巻分であるという。)また、多角数についての著書もあるという。
最終定理を含めてフェルマーが余白に書き込みをしたのは、Claude-Gaspard Bachet de Méziriac〔クロード=ガスパール・バシェ・ド・メジリアク、フランスの言語学者・古典学者〕によるラテン語版『算術』である。
彼は1次方程式と2次方程式の研究も行っている。たとえば、「2数の和は10で、その2乗の差は40である。2数はそれぞれいくらか?」という問題を次のよう解いている。
今2数をそれぞれ 5+xと 5-x とすれば、
題意により、 (5+x)²-(5-x)²=40
∴ 20x=40 よって x=2
したがって、2数は 5+2=7 と 5-2=3 である。
Diophantus〔ディオファントス〕はまた、種々の技巧を凝らして2次方程式を解くことを考えているが、布の数が欠けており、一貫した方法もなかったので、2次方程式の一般的解法は、後のインド人を俟たなければならなかった。
ディオファントスの墓碑銘として知られる問題がある。ギリシァのアテネが地中海を支配していたころ、フェニキア(今のパレスチナ)で発見された石板に刻まれていた古代ギリシアの詞華集の中にある、彼の生涯に関する風刺詩なのだそうだ。曰く、
「ディオファントスの人生は、6分の1が少年期、12分の1が青年期であり、その後に人生の7分の1が経って結婚し、結婚して5年で子供に恵まれた。ところがその子はディオファントスの一生の半分しか生きずに世を去った。自分の子を失って4年後にディオファントスも亡くなった。 ディオファントスは何歳まで生きたか?」
「12分の1」が“頬ヒゲを蓄えるまでの期間”を表して「7分の1」の後に来る話もある。いずれにせよ解は変わらない。
容易に1次方程式を立てて解くことができる。
1/6・x+1/12・x+1/7・x+5+1/2・x+4=x
これをまとめて
3x/28=9 ∴ x=84 となり、84歳という解が得られる。
なお、『Almagest』の本来の書名はギリシャ語で(Mathematike Syntaxis、Mathematical Treatise、数学全書)意味する語であり、通称として(He Megale Syntaxis、The Great Treatise、大全書)が用いられており、アラビア語に翻訳された際に付いた定冠詞Alが、ラテン語に再翻訳されたときにもそのまま残り、Syntaxis(Treatise)が省略されて『Almagest』(The-greatest、最大)になったという。このことからもわかるように、『Almagestアルマゲスト』は当時は数学書として扱われており、球面幾何学など最先端の数学的な内容を含んでいた。
また、著書『Tetrabiblos〔テトラビブロス、四つの書〕』は、占星術の古典として知られている。
ほかに、平行線の公理に関する著書や音楽に関する著書もあったという。
音楽については、音程を二つの音の数比で表すピュタゴラス派の方法論を批判的に継承した。定性的な方法を示した古典期のAristoxenos〔アリストクセノス、前4世紀後半ごろの古代ギリシアの哲学者,音楽理論家〕の『ハルモニア原論』を新ピュタゴラス派(ピュタゴラス派の伝統は紀元前4世紀の末に一度途切れている)の立場から痛烈に批判し、独自の見解を提起した『Elementa harmonica〔ハルモニア論〕』(全三巻)を著したという。
19世紀になり、の観測結果を再調査した天文学者らは、結果の中にある誤差を発見。古代天文学と比べても観測地点や観測時間が間違っているなどミスの多いものだった。Ptolemaeus(プトレマイオス)が行ったとされる天体観測は、プトレマイオス観測以前のロードス島、ヒッパルコスの観測を丸ごと盗用したものであると指摘している天文学者もあるという。
天文学の研究は、その後Menelaus〔メネラウス、AD70?~140?年ごろ〕とClaudius Ptolemaeus〔クラウディオス・プトレマイオス、AD83?~168?年ごろ、英語ではPtolemy (トレミー)〕によって受け継がれた。
 Menelaus(メネラウス)はギリシャの数学者、天文学者であり。直線の類似物として、曲面上の測地線を始めて考察し、Sphaerica (スファーノリカ、「球面論」3巻) がアラビア語の翻訳で生き延びた唯一つの著作物である。メネラウスは三角法の歴史に登場し、また月のクレーターに名前を残しているが、その他のことについての詳細は不明である。
Menelaus(メネラウス)はギリシャの数学者、天文学者であり。直線の類似物として、曲面上の測地線を始めて考察し、Sphaerica (スファーノリカ、「球面論」3巻) がアラビア語の翻訳で生き延びた唯一つの著作物である。メネラウスは三角法の歴史に登場し、また月のクレーターに名前を残しているが、その他のことについての詳細は不明である。
 「1直線が⊿ABCの3辺BC、CA、AB またはその延長とそれぞれP、Q、Rで交われば
「1直線が⊿ABCの3辺BC、CA、AB またはその延長とそれぞれP、Q、Rで交われば
BP/PC・CQ/QA・QR/RB=1 である」という、メネラウスの定理は有名で、高校の幾何で習った方もいるのではなかろうか。(左図参照)
BP/PC・CQ/QA・QR/RB=1 である」という、メネラウスの定理は有名で、高校の幾何で習った方もいるのではなかろうか。(左図参照)
蒸気の圧力を利用したさまざまな仕掛けも考案したが、自らが位置を変えて運動する蒸気機関は作らなかった。主な発明に、蒸気タービンや、蒸気を使って自動で開く扉などがある。
※ aeolos(アイオロス)の球〔aeolipile(イーエウリーパイル〕またはHero engine〔ヘロンの蒸気機関〕は、熱することでロケットのように噴射して回転するジェットエンジンである。紀元1世紀ごろ、Alexandria(アレキサンドリア)のHeron(ヘロン)がこの装置を文献に記し、多くの文献が彼が発明者だとしている。ヘロンの描いたアイオロスの球は、世界初の蒸気機関または蒸気タービンとされている。"aeolipile" の語源はギリシア語の "aeolos"(アイオロス)と "pila"(球)で、aeolos(アイオロス)はギリシア神話の風の神である。
ヘロンは、より実用的にその作り方から説明している。曰く、
ラテン語の写本(1583年)が、ローマの国立図書館に収蔵されているという。
サイフォンと見なせばそれほど不思議ではないが、水鉢と下の箱をつなぐパイプを外し、別の水源から下の箱に水を供給しても、2つの箱の中の空気圧によってその水源の水位以上に水が持ち上がる。この装置は「ヘロンのサイフォン」とも呼ばれている。
水鉢から下に落ちる水の位置エネルギーが下の箱から上の箱に伸びるパイプの空気圧(この部分では空気しか上に移動しない)に変換され、上の箱の水を水鉢の水位以上に押し上げる。
噴水の高さは、水鉢から下の箱までの高低差とほぼ同じになる。最大限に効果を上げるには、上の箱を水鉢のすぐ下に配置し、下の箱はなるべく下に離すのがよい。
上の箱の水位が低くなって、噴水用パイプに水が入らなくなると、噴水が止まる。再び噴水を噴き出させるには、下の箱の水を捨て、上の箱と水鉢を水で満たす必要がある。こうして水を高い位置に戻すことで位置エネルギーを与えたことになる。(左図参照)
2次方程式はエジプトやバビロニアの記録にも断片的に現われているが、これを初めて本格的に取り扱ったのはおそらくHeron(ヘロン)であろうという。彼は、
「1つの正方形がある。その面積と周の和は896である。正方形の1辺はいくらか?」という問題を次のように解いている。
正方形の1辺をxとすれば、題意によって x²+4x=896
この両辺に4をくわえれば、 x²+4x+4=896+4
∴ (x+2)²=900
よって、 x+2=30 ∴ x=28 したがって 正方形の1辺は 28 である。
この場合 x+2=±30 とする必要はないわけである。なぜなら、x は正の数に限るからである。
Heronの生没年については諸説あり、紀元前2世紀ごろとする説から、3世紀前半ごろとする説まである。「Ktesibios(クテシビオス)の弟子」というのが正しいとすると、紀元前2世紀後半から紀元前1世紀ごろの人物、と言うことになる。ブリタニカ百科事典では、著作で62年に見られた月食に言及している、として1世紀ごろの人物としている(なお、現在の版ではこの記述は削除されているが、少なくとも62年に生きていた、としている)。
著書が現存せず、どのような説を唱えたのかははっきりしない。Ptolemy〔トレミー、ギリシア名はPtolemaios(プトレマイオス)〕の48星座とかみのけ座の合わせて49星座を決定したのもHipparchus(ヒッパルコス)だと言われるが、はっきりと分かっている業績は、46星座の決定のみである。Claudius Ptolemaeus〔クラウディオス・プトレマイスオ、83?~168?年、古代ローマの天文学者、数学者、地理学者、占星術師)の『Almagest(アルマゲスト)』で、最も引用回数の多いのがHipparchus(ヒッパルコス)であることから、天動説を含む古代の天文学の体系を成立させたのはHipparchus(ヒッパルコス)であるという説がある。これは広く支持されているが、決定的な証明がなされていない。
※ HipparcosはHigh Precision Parallax Collecting Satellite(ハイ プレシジャン パララックス コレクティング サテライト、高精度視差収集人工衛星)の略
Hipparchus(ヒッパルコス)主な業績
・ 恒星を1等星から6等星までの6段階に分けた。これは若干形を変え、視等級として現代でも使われている。
・ 三角法による測量を行った。
・ 歳差による春分点移動を発見した。
・ メトン周期の改良。
※ Metonic cycle〔メトン周期〕:19暦年を235暦月,6940日に等置する周期。ギリシアの科学者Metōn〔メトン、BC5世紀のギリシャの数学者、天文学者、技術者〕が前433年に当時行われていた太陰太陽暦の誤りを正すために提案したもの。12ヵ月を1年とする平年が12回,13ヵ月の閏年が7回ある。そのうち30日の大の月が125,29日の小の月が110である。中国でも章法といって19年7閏の法が紀元前より知られていた。正しい値は19太陽年は6939.6018日,235朔望月は6939.6884日である。
プロフィール
ハンドルネーム:
目高 拙痴无
年齢:
93
誕生日:
1932/02/04
自己紹介:
くたばりかけの糞爺々です。よろしく。メールも頼むね。
sechin@nethome.ne.jp です。
sechin@nethome.ne.jp です。
カレンダー
| 12 | 2026/01 | 02 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
最新コメント
[enken 02/23]
[中村東樹 02/04]
[m、m 02/04]
[爺の姪 01/13]
[レンマ学(メタ数学) 01/02]
[m.m 10/12]
[爺の姪 10/01]
[あは♡ 09/20]
[Mr.サタン 09/20]
[Mr.サタン 09/20]
最新トラックバック
ブログ内検索
カウンター
