瘋癲爺 拙痴无の戯言・放言・歯軋り
今年は7月22日が土用の丑の日である。かつて、兼愛塾の臨海学校で、西伊豆の長松寺で先発隊の準備を終えると、臨海学校参加の生徒を迎えに爺1人で一旦帰京したが、この時の夕食は決まって「うなぎ」を食った。最近ではスーパーでも品薄でうなぎが高騰しているという。量が半減した上に価格は5割り増しになった所もあるという。はてさて、ニホンウナギは今年の夏で見納めになるのか?
今朝のウェブニュースより、
 ウナギ瀬戸際 それでも食卓へ ―― 国際自然保護連合は今月、ニホンウナギを絶滅危惧種に指定するか検討に入った。国際取引を規制するワシントン条約の議論にも影響する。日本では今、海外種の輸入や完全養殖事業化の動きが進む。我々はどこまでウナギを消費し続けるのだろうか。/ 「近い将来、スーパーの店頭からニホンウナギが消えるかもしれない」。今年、ウナギ業界の関係者からこんな声を聞くようになった。/ウナギ自体が消えるというわけではない。資源が枯渇し、相場が高騰しているニホンウナギに代わる新顔が、量販店での「お手ごろなウナギ」の主流になる可能性があるというのだ。/筆頭候補は東南アジアに生息するビカーラ種。既に大手スーパーの店頭にも登場している。ニホンウナギに比べると体長が短く、皮が厚いが、かば焼きになると簡単には見分けがつかない。価格は1尾千円以下。ニホンウナギより500円以上安い。/7月22日は需要のピークの土用の丑(うし)。インドネシアでビカーラ種の養殖・加工を手がけるインダスト(熊本県玉名市)の中川勝也社長は「引き合いは強い。色々な取引先からあるだけすべて欲しいと言われる」と話す。/ビカーラ種の養殖・加工はインドネシア以外に、日本や中国でも始まっている。混乱を避けるため、水産庁は5月、ニホンウナギを原料にした国産かば焼き製品には「ニホンウナギ」と明記するよう通達を出した。
ウナギ瀬戸際 それでも食卓へ ―― 国際自然保護連合は今月、ニホンウナギを絶滅危惧種に指定するか検討に入った。国際取引を規制するワシントン条約の議論にも影響する。日本では今、海外種の輸入や完全養殖事業化の動きが進む。我々はどこまでウナギを消費し続けるのだろうか。/ 「近い将来、スーパーの店頭からニホンウナギが消えるかもしれない」。今年、ウナギ業界の関係者からこんな声を聞くようになった。/ウナギ自体が消えるというわけではない。資源が枯渇し、相場が高騰しているニホンウナギに代わる新顔が、量販店での「お手ごろなウナギ」の主流になる可能性があるというのだ。/筆頭候補は東南アジアに生息するビカーラ種。既に大手スーパーの店頭にも登場している。ニホンウナギに比べると体長が短く、皮が厚いが、かば焼きになると簡単には見分けがつかない。価格は1尾千円以下。ニホンウナギより500円以上安い。/7月22日は需要のピークの土用の丑(うし)。インドネシアでビカーラ種の養殖・加工を手がけるインダスト(熊本県玉名市)の中川勝也社長は「引き合いは強い。色々な取引先からあるだけすべて欲しいと言われる」と話す。/ビカーラ種の養殖・加工はインドネシア以外に、日本や中国でも始まっている。混乱を避けるため、水産庁は5月、ニホンウナギを原料にした国産かば焼き製品には「ニホンウナギ」と明記するよう通達を出した。
暑さの盛りの土用の丑にウナギを食べる慣習は商売上の戦略から始まった。ウナギ屋の店主から客足が落ちる夏の集客策を請われた江戸時代の知識人・平賀源内は、丑の日にウのつくウナギを食べる夏バテ対策を提案したといわれる。元来、ウナギの旬は冬眠に向けてエサを食べ込む秋だったのだ。/現在、日本人が食べているウナギは99%以上が養殖物だ。養殖に使う稚魚のシラスウナギは日本の南方2500キロの西マリアナ海域でふ化した後、海流に乗り、冬から春に日本の河川にやってくる。養殖業者はこの時期に捕れたシラスを仕入れ、成魚に育てて出荷する。ビニールハウスでボイラーをたき、エサを大量に与え、自然界では3~10年かかる工程を半年でこなす力業。高値で売れる丑の日に間に合わせるためだ。/1990年代から2000年代前半にかけて、低価格を武器にした中国産の冷凍かば焼きの輸入が急増した。日本でも負けじと大型加工場が次々と建った。大型スーパーやファストフードもお手ごろ価格のウナギを扱い始め、晴れの日の食材だったウナギは、ワンコインで調達できる日常食に様変わりした。
行き過ぎた商業主義のツケが噴出したのは一昨年だ。需要期の夏を過ぎてもウナギの値段が下がらなくなった。その冬、稚魚が深刻な不漁になるとウナギ相場は高騰した。昨年春には前年同期の2倍になり、ウナギ店の値上げや廃業が相次いだ。/稚魚の不漁は過去の乱獲が原因とみられている。ニホンウナギの後釜と期待されるビカーラ種にしても、資源の状況は未知数だ。ニホンウナギを絶滅の危機に追い込んだ大量漁獲、安値販売を繰り返す愚は何としても避けたい。/ニホンウナギの稚魚を人工的に育てる技術は確立されている。しかし、コストの高さを考えれば天然の稚魚に頼らない養殖の早期実現は非現実的だ。海洋環境の変化により、ニホンウナギの資源が急回復する可能性もなくはないが「それをあてにしてシラスを捕り続けるのは万馬券を狙って原資を減らし続けるようなもの」(北里大学海洋生命科学部の吉永龍起講師)。当たるのが先か、破産が先か。/安いウナギが大量に出回る時代は当分来ないとあきらめた方がいい。今、消費者としてできることは、ウナギを晴れの日の食材として認識し直し、特別な日に、相応の対価を払って食べることだ。ウナギは元来、日常食にはもったいない存在なのである。 (日本経済新聞 7月19日)
今朝のウェブニュースより、
暑さの盛りの土用の丑にウナギを食べる慣習は商売上の戦略から始まった。ウナギ屋の店主から客足が落ちる夏の集客策を請われた江戸時代の知識人・平賀源内は、丑の日にウのつくウナギを食べる夏バテ対策を提案したといわれる。元来、ウナギの旬は冬眠に向けてエサを食べ込む秋だったのだ。/現在、日本人が食べているウナギは99%以上が養殖物だ。養殖に使う稚魚のシラスウナギは日本の南方2500キロの西マリアナ海域でふ化した後、海流に乗り、冬から春に日本の河川にやってくる。養殖業者はこの時期に捕れたシラスを仕入れ、成魚に育てて出荷する。ビニールハウスでボイラーをたき、エサを大量に与え、自然界では3~10年かかる工程を半年でこなす力業。高値で売れる丑の日に間に合わせるためだ。/1990年代から2000年代前半にかけて、低価格を武器にした中国産の冷凍かば焼きの輸入が急増した。日本でも負けじと大型加工場が次々と建った。大型スーパーやファストフードもお手ごろ価格のウナギを扱い始め、晴れの日の食材だったウナギは、ワンコインで調達できる日常食に様変わりした。
行き過ぎた商業主義のツケが噴出したのは一昨年だ。需要期の夏を過ぎてもウナギの値段が下がらなくなった。その冬、稚魚が深刻な不漁になるとウナギ相場は高騰した。昨年春には前年同期の2倍になり、ウナギ店の値上げや廃業が相次いだ。/稚魚の不漁は過去の乱獲が原因とみられている。ニホンウナギの後釜と期待されるビカーラ種にしても、資源の状況は未知数だ。ニホンウナギを絶滅の危機に追い込んだ大量漁獲、安値販売を繰り返す愚は何としても避けたい。/ニホンウナギの稚魚を人工的に育てる技術は確立されている。しかし、コストの高さを考えれば天然の稚魚に頼らない養殖の早期実現は非現実的だ。海洋環境の変化により、ニホンウナギの資源が急回復する可能性もなくはないが「それをあてにしてシラスを捕り続けるのは万馬券を狙って原資を減らし続けるようなもの」(北里大学海洋生命科学部の吉永龍起講師)。当たるのが先か、破産が先か。/安いウナギが大量に出回る時代は当分来ないとあきらめた方がいい。今、消費者としてできることは、ウナギを晴れの日の食材として認識し直し、特別な日に、相応の対価を払って食べることだ。ウナギは元来、日常食にはもったいない存在なのである。 (日本経済新聞 7月19日)
PR
今朝のウェブニュースより
モンゴルで遊牧民の巨大碑文発見 「我が土地よ、ああ」 ―― 8世紀中ごろのトルコ系遊牧民族「突厥(とっけつ)」の巨大な碑文をモンゴル東部の草原で発見した、と大阪大大学院の大澤孝教授(古代トルコ史)が16日発表した。中国の隋・唐の各帝国と時に対立し、時に結びながら中央アジアを支配した突厥の国家体制や制度を解明する貴重な史料となりそうだ。/大澤教授とモンゴル科学アカデミー考古学研究所は5月、ウランバートルの南東約400キロにあるデレゲルハーン山近郊のドンゴイン・シレーと呼ばれる遺跡で、それぞれ全長約4メートルと約3メートルの碑文の残片を発見した。計20行、2832文字の古代トルコ文字(突厥文字)が刻まれ、解読の結果、「我が家よ、ああ」「我が土地よ、ああ」など、死者が家族や故郷との別れを惜しむ文面だった。刻まれた部族の紋章から、突厥第2帝国(682~744年)の王家、アシナ氏の一員の墓碑とみられる。/突厥は、中央ユーラシアの遊牧民族で最も古くに独自の言語と文字を残した。著名な3大碑文(ビルゲ可汗〈カガン〉、キョルテギン、トニュクク〕が19世紀末にモンゴル中部で見つかっているが、それらに匹敵する碑文の発見は約120年ぶり。大澤教授は「地中に埋まっている部分に被葬者の生前の事績が記されている可能性がある」と話す。


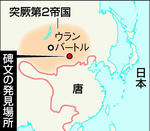
※ 突厥:突厥〔とっけつ、英語ではTürük(テュルク)、トルコ語ではGöktürk(ギョクテュルク)〕は、6世紀に中央ユーラシアに存在したテュルク系遊牧国家。もともとはジュンガル盆地北部からトルファン北方の山麓にかけて住んでいた部族で、柔然〔じゅうぜん、5世紀から6世紀に欠けてモンゴル高原を支配した遊牧国家〕の隷属の下でアルタイ山脈の南麓へ移住させられ鍛鉄奴隷として鉄工に従事したが、552年に柔然から独立すると、部族連合である突厥可汗(ハガン)国(突厥帝国などと呼ばれることもある)を建て、中央ユーラシアの覇者となる。582年には内紛によって東西に分裂した。/6世紀~8世紀半ばにモンゴル高原から中央アジアにかけての地域を支配したテュルク系(トルコ系)遊牧騎馬民族とその国家。突厥という言葉自体がテュルクの音写表記。独自の文字をもっていたことで知られている。/その首長は可汗(ハガン)と呼ばれた。/アルタイ山脈の麓に住んでいて、当初はモンゴル高原に勢力を伸ばした柔然(じゅうぜん)に従属していたが、6世紀中頃から徐々に勢力を強め、有力氏族であった阿史那(あしな)氏の族長土門〔ブミン、?~552ねん〕は同じテュルク系である鉄勒諸部族を服属させると552年柔然の敕連頭兵伐可汗(ちょくれんとうへいはつかがん)阿那瓌〔あなかい、? - 552年〕を破って独立した。土門は即位して、伊利(イリク)可汗となった。その後三代木杆可汗〔ぼくかんかがん、?~572年〕はモンゴル高原の柔然を滅ぼし、契丹を討ち、キルギスを併せ、ササン朝ペルシャと結んで隣接するエフタルを滅ぼし、大勢力を築き上げた。その領土はモンゴル高原からカスピ海北岸のキプチャク草原に至り、ソグド人などの定住民が居住する中央アジアのオアシス地帯までも支配する大帝国を築き、その支配のもとで中央ユーラシア全域に及ぶテュルク世界の原型が形作られた。/その後、隋の離間策によって東西に分裂した。
モンゴルで遊牧民の巨大碑文発見 「我が土地よ、ああ」 ―― 8世紀中ごろのトルコ系遊牧民族「突厥(とっけつ)」の巨大な碑文をモンゴル東部の草原で発見した、と大阪大大学院の大澤孝教授(古代トルコ史)が16日発表した。中国の隋・唐の各帝国と時に対立し、時に結びながら中央アジアを支配した突厥の国家体制や制度を解明する貴重な史料となりそうだ。/大澤教授とモンゴル科学アカデミー考古学研究所は5月、ウランバートルの南東約400キロにあるデレゲルハーン山近郊のドンゴイン・シレーと呼ばれる遺跡で、それぞれ全長約4メートルと約3メートルの碑文の残片を発見した。計20行、2832文字の古代トルコ文字(突厥文字)が刻まれ、解読の結果、「我が家よ、ああ」「我が土地よ、ああ」など、死者が家族や故郷との別れを惜しむ文面だった。刻まれた部族の紋章から、突厥第2帝国(682~744年)の王家、アシナ氏の一員の墓碑とみられる。/突厥は、中央ユーラシアの遊牧民族で最も古くに独自の言語と文字を残した。著名な3大碑文(ビルゲ可汗〈カガン〉、キョルテギン、トニュクク〕が19世紀末にモンゴル中部で見つかっているが、それらに匹敵する碑文の発見は約120年ぶり。大澤教授は「地中に埋まっている部分に被葬者の生前の事績が記されている可能性がある」と話す。
※ 突厥:突厥〔とっけつ、英語ではTürük(テュルク)、トルコ語ではGöktürk(ギョクテュルク)〕は、6世紀に中央ユーラシアに存在したテュルク系遊牧国家。もともとはジュンガル盆地北部からトルファン北方の山麓にかけて住んでいた部族で、柔然〔じゅうぜん、5世紀から6世紀に欠けてモンゴル高原を支配した遊牧国家〕の隷属の下でアルタイ山脈の南麓へ移住させられ鍛鉄奴隷として鉄工に従事したが、552年に柔然から独立すると、部族連合である突厥可汗(ハガン)国(突厥帝国などと呼ばれることもある)を建て、中央ユーラシアの覇者となる。582年には内紛によって東西に分裂した。/6世紀~8世紀半ばにモンゴル高原から中央アジアにかけての地域を支配したテュルク系(トルコ系)遊牧騎馬民族とその国家。突厥という言葉自体がテュルクの音写表記。独自の文字をもっていたことで知られている。/その首長は可汗(ハガン)と呼ばれた。/アルタイ山脈の麓に住んでいて、当初はモンゴル高原に勢力を伸ばした柔然(じゅうぜん)に従属していたが、6世紀中頃から徐々に勢力を強め、有力氏族であった阿史那(あしな)氏の族長土門〔ブミン、?~552ねん〕は同じテュルク系である鉄勒諸部族を服属させると552年柔然の敕連頭兵伐可汗(ちょくれんとうへいはつかがん)阿那瓌〔あなかい、? - 552年〕を破って独立した。土門は即位して、伊利(イリク)可汗となった。その後三代木杆可汗〔ぼくかんかがん、?~572年〕はモンゴル高原の柔然を滅ぼし、契丹を討ち、キルギスを併せ、ササン朝ペルシャと結んで隣接するエフタルを滅ぼし、大勢力を築き上げた。その領土はモンゴル高原からカスピ海北岸のキプチャク草原に至り、ソグド人などの定住民が居住する中央アジアのオアシス地帯までも支配する大帝国を築き、その支配のもとで中央ユーラシア全域に及ぶテュルク世界の原型が形作られた。/その後、隋の離間策によって東西に分裂した。
いやはや、白鵬と琴奨菊には破れたものの中日を過ぎての6勝2敗は立派。1988年生まれの24歳というから、順調に成長すれば、綱取りも夢ではあるまい。まあ、この爺がくたばらない内に綱取りを果たしてもらいたいものだ。
今朝のウェブニュースより
折り返し、S氏から電話。ちょうど奥様が用事で市役所に向かわれるところであったそうだ。でも、バス停でニュースを知り、無事現場に遭遇することはなかったとのこと。何より。
今朝のウェブニュースより
当時、現場にいた市の職員などによりますと、高橋容疑者は「俺の人生むちゃくちゃや。お前らが差し押さえするからこうなったんや。俺の答えはこれや」と叫んで、火炎瓶を投げつけたということです。/警察は、当時の状況や動機を調べています。
市長「暴力絶対許されない」:宝塚市の中川智子市長は、「火炎瓶が投げ込まれた場所には書類が多かったため、あっという間に燃え広がったと、現場にいた職員から聞いている。職員や市民を守りきれなくてつらい。暴力は絶対許されない。何があったか、しっかり検証していきたい」と話していました。
市役所きょうの業務取りやめ:宝塚市によりますと、12日は火災の対応を除いて市役所本庁舎での窓口での業務や事務作業は、すべて取りやめることが決まったということです。 〔NHK NEWS WEB 7月12日 12時29分〕
Brahmagupta(ブラーマグプタ)が7世紀に発展させた天文モデルを使い、Bhāskara(バースカラ)2世は恒星年(地球が太陽の周りを一周するのにかかる時間)の長さを(『Surya Siddhanta(スールヤ・シッダーンタ)』と同じく)365.2588日とするなど、様々な天文学上の量を定義した。現在の測定値は365.2563日で、その差異はたったの3.5分である。
※ 今日までに知られているインドで生み出された天文学に関する最初の重要な著作は、Surya Siddhanta〔スールヤ・シッダーンタ、5世紀初め頃に書かれたものか?〕であろうが、現在の人びとには、後の時代の写本でしか知ることができない。
彼の天文学の著書『Siddhānta Shiromani(シッダーンタ・シロマーニ)』は2つの部分からなる。前半は数学的天文学であり、後半は球面を扱っている。
前半部の12章では、次のような内容を扱っている。
・惑星の平均経度、 ・惑星の真の経度、 ・日周運動の3つの問題 、 ・惑星直列、 ・月食
・日食、 ・惑星の緯度 ・出没方程式 、 ・月の満ち欠け、 ・2つの惑星の合 ・惑星と恒星の合
後半は球面に関する13章からなる。次のような内容を扱っている。
・球面の研究への賛辞、 ・球面の性質、 ・宇宙誌と地理学、 ・惑星の平均運行速度
・惑星の離心周転円モデル、 ・天球儀、 ・球面三角法、 ・楕円の計算、 ・惑星の可視性
・月の満ち欠けの計算、 ・天文用器具、 ・季節、 ・天文計算の問題
1150年、Bhāskara(バースカラ)2世は永久に回り続ける車輪について記述しており、永久機関の古い例の1つとなっている。
 Bhāskara(バースカラ)2世は Yasti―yantra と呼ばれる測定器具を使っていた。単純な棒状になったり、V字型に変形させたりでき、定規と組み合わせて角度を測るのに主に使ったという。(左図参照)
Bhāskara(バースカラ)2世は Yasti―yantra と呼ばれる測定器具を使っていた。単純な棒状になったり、V字型に変形させたりでき、定規と組み合わせて角度を測るのに主に使ったという。(左図参照)
※ 今日までに知られているインドで生み出された天文学に関する最初の重要な著作は、Surya Siddhanta〔スールヤ・シッダーンタ、5世紀初め頃に書かれたものか?〕であろうが、現在の人びとには、後の時代の写本でしか知ることができない。
彼の天文学の著書『Siddhānta Shiromani(シッダーンタ・シロマーニ)』は2つの部分からなる。前半は数学的天文学であり、後半は球面を扱っている。
前半部の12章では、次のような内容を扱っている。
・惑星の平均経度、 ・惑星の真の経度、 ・日周運動の3つの問題 、 ・惑星直列、 ・月食
・日食、 ・惑星の緯度 ・出没方程式 、 ・月の満ち欠け、 ・2つの惑星の合 ・惑星と恒星の合
後半は球面に関する13章からなる。次のような内容を扱っている。
・球面の研究への賛辞、 ・球面の性質、 ・宇宙誌と地理学、 ・惑星の平均運行速度
・惑星の離心周転円モデル、 ・天球儀、 ・球面三角法、 ・楕円の計算、 ・惑星の可視性
・月の満ち欠けの計算、 ・天文用器具、 ・季節、 ・天文計算の問題
1150年、Bhāskara(バースカラ)2世は永久に回り続ける車輪について記述しており、永久機関の古い例の1つとなっている。
Bhāskara2世の数学への貢献には、以下のようなものがある。
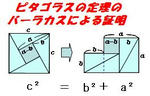 ・ ピタゴラスの定理の証明。同じ領域の面積を2種類の方法で計算し、項を相殺させて消すことで
・ ピタゴラスの定理の証明。同じ領域の面積を2種類の方法で計算し、項を相殺させて消すことで
a² + b² = c² という式を導いた。 (左図参照)
・ 『Lilāvati(リーラーヴァティ)』において、二次方程式、三次方程式、四次方程式の解を示した。
・ 線形および二次の方程式で整数解を求める方法(クッタカ法)。17世紀ルネサンス期のヨーロッパの数学者と同じ方法である。
・ ax²+bx+c=y という形式の方程式を解くChakravala(チャクラバーラ)法 。この方程式は1657年にWilliam Brouncker〔ウィリアム・ブラウンカー、1620?~1684年、イングランド人数学者、医師〕が解いたとされていたが、彼の方法はChakravala(チャクラバーラ)法よりも複雑だった。
・ ペル方程式と呼ばれるx²− ny²=1 という形式の方程式の整数解を求める方法を示した。
・ 61x² + 1 = y² のような二次のディオファントス方程式の解法。この方程式は1657年、フランスの数学者Pierre de Fermat〔ピエール・ド・フェルマー、1607年末または1608年初頭~1665年、フランスの数学者。「数論の父」とも呼ばれる。ただし、職業は弁護士であり、数学は余暇に行ったものであるという〕が問題として提示したが、ヨーロッパでこの解法を明らかにしたのはLeonhard Euler〔レオンハルト・オイラー, 1707~1783年、数学者・物理学者であり、天文学者(天体物理学者)〕で18世紀になってからのことである。
・ 変数が複数ある二次方程式を解き、負数と無理数の解を発見した。
・ 解析学の基本概念。
・ 微分法の基本概念と積分法の元となる貢献。導関数と微分係数を発見。平均値の定理の特殊な場合であるロルの定理を発見。平均値の定理と思われる記述も著作の中に見つかっている。
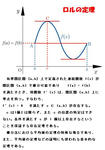 ※ ロルの定理(Rolle's theorem、左図参照) は1691年にフランスの数学者Michel Rolle (ミシェル・ロル、1652~1719年)が著書の「代数学」(Traite d'algebre) で発表されたためにロルの名がついているが、Isaac Newton〔アイザック ニュートン、1642~1727年〕やGottfried Leibniz〔ゴットフリート ライプニッツ、 1646~1716年〕によって微分が発見されるより前の12世紀にインドの天文学者バスカラが同様の定理を述べたとされる。
※ ロルの定理(Rolle's theorem、左図参照) は1691年にフランスの数学者Michel Rolle (ミシェル・ロル、1652~1719年)が著書の「代数学」(Traite d'algebre) で発表されたためにロルの名がついているが、Isaac Newton〔アイザック ニュートン、1642~1727年〕やGottfried Leibniz〔ゴットフリート ライプニッツ、 1646~1716年〕によって微分が発見されるより前の12世紀にインドの天文学者バスカラが同様の定理を述べたとされる。
・ 三角関数の導関数を計算。
・ 『Siddhānta Shiromani(シッダーンタ・シロマーニ)』の中で、いくつかの三角法と共に球面三角法を展開している。
Bhāskara(バースカラ)2世の算術についての著書『Lilāvati(リーラーヴァティ)』は、定義、算術用語、利子計算、算術級数と幾何級数、平面幾何学、立体幾何学、日時計の影、不変方程式の解法、組合せなどを扱っている。
『Lilāvati(リーラーヴァティ)』は13章からなり、算術だけでなく代数学や幾何学も扱い、一部は三角法や求積法を扱っている。具体的には、次のような内容がある。
・ 定義
・ ゼロの性質(除法を含むゼロの演算規則)
・ その他の数に関すること。負数や無理数(冪根)を含む。
・ 円周率の近似値。
・ 算術。乗法や平方など。
・ 利子計算に関する問題。
・ 算術級数と幾何級数。
・ 平面の幾何学。
・ 立体の幾何学。
・ 組合せ数学(順列と組合せ)。
・ 線型および二次の不定方程式の整数解の求め方(クッタカ)。これについては、17世紀ルネサンス期のヨーロッパの数学者と同じ解法を示しており、非常に重要である。バースカラ2世の解法は、アリヤバータなど先人の成果に基づくものだった。
彼の著書は体系化、解法の改善、新たな問題の導入などの点が優れている。さらに『Lilāvati(リーラーヴァティ)』には素晴らしい例題もあり、バースカラ2世は『Lilāvati(リーラーヴァティ)』で学ぶ学生にその内容を具体的に役立てて欲しいと意図していたとも思われる。
『Bijaganita(ビージャガニタ)』(代数学)は12章からなる。正の数に(正と負の)2つの平方根があることを初めて示した文書である。次のような内容を含む。
・正数と負数、 ・ゼロ、 ・未知数、 ・未知の数量の決定、 ・冪根と無理数、
・クッタカ法(不定方程式およびディオファントス方程式の解法)、 ・単純な方程式(二次、三次、四次)
・複数の変数のある単純な方程式、 ・不定二次方程式〔ax² + b = y² という形式のもの〕
・二次、三次、四次の不定方程式の解法、 ・二次方程式、 ・複数の変数のある二次方程式
・複数の変数の積の操作
Bhāskara(バースカラ)2世は ax² + bx + c = y という形式の不定二次方程式の解法としてChakravala(チャクラバーラ)法を導き出した。ペル方程式と呼ばれる Nx² + 1 = y² という形式の問題の整数解を求めるBhāskara(バースカラ)2世の方法も重要である(こちらもChakravala法)という。
 『Siddhānta Shiromani(シッダーンタ・シロマーニ)』〔1150年〕では、三角法を扱っており、正弦関数の数表や各種三角関数の関係も記している。また、いくつかの興味深い三角法に混じって球面三角法も発見している。Bhāskara(バースカラ)2世以前のインドの数学者は三角法を計算の道具としか見ていなかったが、Bhāskara2世自身は三角法に大きな興味を持っていたように思われる。三角関数の加法定理〔左図参照〕といわれる sin(α+β) や sin(α- β) なども扱っている。
『Siddhānta Shiromani(シッダーンタ・シロマーニ)』〔1150年〕では、三角法を扱っており、正弦関数の数表や各種三角関数の関係も記している。また、いくつかの興味深い三角法に混じって球面三角法も発見している。Bhāskara(バースカラ)2世以前のインドの数学者は三角法を計算の道具としか見ていなかったが、Bhāskara2世自身は三角法に大きな興味を持っていたように思われる。三角関数の加法定理〔左図参照〕といわれる sin(α+β) や sin(α- β) なども扱っている。
a² + b² = c² という式を導いた。 (左図参照)
・ 『Lilāvati(リーラーヴァティ)』において、二次方程式、三次方程式、四次方程式の解を示した。
・ 線形および二次の方程式で整数解を求める方法(クッタカ法)。17世紀ルネサンス期のヨーロッパの数学者と同じ方法である。
・ ax²+bx+c=y という形式の方程式を解くChakravala(チャクラバーラ)法 。この方程式は1657年にWilliam Brouncker〔ウィリアム・ブラウンカー、1620?~1684年、イングランド人数学者、医師〕が解いたとされていたが、彼の方法はChakravala(チャクラバーラ)法よりも複雑だった。
・ ペル方程式と呼ばれるx²− ny²=1 という形式の方程式の整数解を求める方法を示した。
・ 61x² + 1 = y² のような二次のディオファントス方程式の解法。この方程式は1657年、フランスの数学者Pierre de Fermat〔ピエール・ド・フェルマー、1607年末または1608年初頭~1665年、フランスの数学者。「数論の父」とも呼ばれる。ただし、職業は弁護士であり、数学は余暇に行ったものであるという〕が問題として提示したが、ヨーロッパでこの解法を明らかにしたのはLeonhard Euler〔レオンハルト・オイラー, 1707~1783年、数学者・物理学者であり、天文学者(天体物理学者)〕で18世紀になってからのことである。
・ 変数が複数ある二次方程式を解き、負数と無理数の解を発見した。
・ 解析学の基本概念。
・ 微分法の基本概念と積分法の元となる貢献。導関数と微分係数を発見。平均値の定理の特殊な場合であるロルの定理を発見。平均値の定理と思われる記述も著作の中に見つかっている。
・ 三角関数の導関数を計算。
・ 『Siddhānta Shiromani(シッダーンタ・シロマーニ)』の中で、いくつかの三角法と共に球面三角法を展開している。
Bhāskara(バースカラ)2世の算術についての著書『Lilāvati(リーラーヴァティ)』は、定義、算術用語、利子計算、算術級数と幾何級数、平面幾何学、立体幾何学、日時計の影、不変方程式の解法、組合せなどを扱っている。
『Lilāvati(リーラーヴァティ)』は13章からなり、算術だけでなく代数学や幾何学も扱い、一部は三角法や求積法を扱っている。具体的には、次のような内容がある。
・ 定義
・ ゼロの性質(除法を含むゼロの演算規則)
・ その他の数に関すること。負数や無理数(冪根)を含む。
・ 円周率の近似値。
・ 算術。乗法や平方など。
・ 利子計算に関する問題。
・ 算術級数と幾何級数。
・ 平面の幾何学。
・ 立体の幾何学。
・ 組合せ数学(順列と組合せ)。
・ 線型および二次の不定方程式の整数解の求め方(クッタカ)。これについては、17世紀ルネサンス期のヨーロッパの数学者と同じ解法を示しており、非常に重要である。バースカラ2世の解法は、アリヤバータなど先人の成果に基づくものだった。
彼の著書は体系化、解法の改善、新たな問題の導入などの点が優れている。さらに『Lilāvati(リーラーヴァティ)』には素晴らしい例題もあり、バースカラ2世は『Lilāvati(リーラーヴァティ)』で学ぶ学生にその内容を具体的に役立てて欲しいと意図していたとも思われる。
『Bijaganita(ビージャガニタ)』(代数学)は12章からなる。正の数に(正と負の)2つの平方根があることを初めて示した文書である。次のような内容を含む。
・正数と負数、 ・ゼロ、 ・未知数、 ・未知の数量の決定、 ・冪根と無理数、
・クッタカ法(不定方程式およびディオファントス方程式の解法)、 ・単純な方程式(二次、三次、四次)
・複数の変数のある単純な方程式、 ・不定二次方程式〔ax² + b = y² という形式のもの〕
・二次、三次、四次の不定方程式の解法、 ・二次方程式、 ・複数の変数のある二次方程式
・複数の変数の積の操作
Bhāskara(バースカラ)2世は ax² + bx + c = y という形式の不定二次方程式の解法としてChakravala(チャクラバーラ)法を導き出した。ペル方程式と呼ばれる Nx² + 1 = y² という形式の問題の整数解を求めるBhāskara(バースカラ)2世の方法も重要である(こちらもChakravala法)という。
代々、宮廷学者の地位を世襲しており、Bhāskara(バースカラ)の息子やその子孫もその地位を継承していることが記録に残っている。父 Mahesvara(マヘーシュヴァラ)は占星術師で、Bhāskara(バースカラ)に数学を教え、Bhāskara(バースカラ)はそれを息子 Loksamudra に継承させた。Loksamudra の息子は1207年に学校設立を助け、そこでBhāskara(バースカラ)の書いた文書の研究を行った。
Bhāskara(バースカラ)は、12世紀の数学および天文学の発展に大きな業績を残した。主な著書として、『Lilavati 〔リーラーヴァティ、主に算術を扱っている〕』、『Bijaganita 〔ビージャガニタ、代数学〕』、『Siddhānta Shiromani 〔シッダーンタ・シロマーニ、1150年〕』がある。『Siddhānta Shiromani〔シッダーンタ・シロマーニ〕』は Goladhyaya(球面)と Grahaganita(惑星の数学)の2部構成になっている。
Bhāskara(バースカラ)2世の算術の本は、彼の娘Lilāvati(リーラーヴァティ)のために書かれたという伝説がある。ペルシア語版の『Lilāvati(リーラーヴァティ)』に書かれていた物語は、Bhāskara2世がLilāvatiのhoroscope(ホロスコープ)を研究して占ってみたところ、娘がある特定の時刻に結婚しないと彼女の夫が結婚後間もなく死ぬとでた、というものである。娘にその正しい時刻を警告するため、Bhāskara2世破水の入った容器を置き、その上に底に小さな穴の開いたカップを浮かべ、ちょうどよい時刻にカップが沈むように設定した。そして、Lilāvati(リーラーヴァティ)にはそれに近づかないよう警告した。しかし娘は奇妙に思ってそれを覗き込み、鼻につけていた真珠がカップに落ち、沈み方が変わってしまった。そのため、結婚が間違った時間に執り行われ、彼女は間もなく未亡人となったという。
※ ホロスコープ(horoscope、チャート)は占星術における各個人を占うための天体の配置図。惑星、黄道十二宮、十二室、角度の4つの要素で構成される。
Bhāskara(バースカラ)2世は、有限の数をゼロで割ると(ゼロ除算)無限大になるという近代的な数学と同じ考え方をしていた。
Brahmagupta(ブラーマグプタ、598~668年?)はインドの数学者・天文学者。「ブラマグプタ」とも発音される。その著作は、イスラーム世界やヨーロッパにインド数学や天文学を伝える役割を果たした。
628年に、総合的な数理天文書『Brahmasphutasiddhanta〔ブラーマ・スプタ・シッダーンタ、「宇宙の始まり」という意味〕』を著した。この中の数章で数学が扱われており、第12章はGanita〔ガニタ、算術〕、第18章はkuttaka〔クッタカ、代数〕にあてられている。Kuttaka(クッタカ)という語は、もとは「粉々に砕く」という意味だったが、のちに係数の値を小さくしてゆく逐次過程の方法を意味するようになり、代数の中で不定解析を表すようになった。この書では、 0 と負の数にも触れていて、その算法は現代の考え方に近い(ただし 0 ÷ 0 = 0 と定義している点は現代と異なっている)。Brahmagupta(ブラーマグプタ)の問題と呼ばれる二次不定方程式(x²- 92y² = 1)の最小整数解〔x = 1151, y = 120〕も同書で示している。また、665年に著した天文書『カンダ・カードヤカ』では、三角法をVarahamihira〔ヴァラーハミヒラ、505~587年、古代インドの天文学者、占星術師〕の時代からさらに発展させた。
Brahmagupta(ブラーマグプタ)の二平方恒等式と呼ばれる式もある。2つの平方数の和で表される2つの数の積が、2つの平方数の和で表せる事を示す式である。
(a² + b²)(c² + d²) = 〔ac - bd)² + (ad + bc)² = (ac + bd)² + (ad - bc)²
この等式は、Leonardo Fibonacci〔レオナルド・フィボナッチ、1170?~1250年?頃、中世で最も才能があったと評価されるイタリアの数学者〕が彼の著書に書いたことでFibonacci(フィボナッチ)の二平方恒等式とも呼ばれる。先に挙げた3世紀の数学者Diophantus(ディオファントス)もこの恒等式を知っていたと見られる。先のBrahmagupta(ブラーマグプタ)の公式とHeron(ヘロン)の公式の関係のように、このの二平方恒等式はLeonhard Euler〔レオンハルト・オイラー、 1707~1783年、スイスの数学者・物理学者であり、天文学者(天体物理学者)〕四平方恒等式に拡張される。
Āryabhaṭa(アリヤバータ、476~550年頃〕は5世紀末に生まれたインドの数学者、天文学者である。
 Āryabhaṭa(アリヤバータ)が活動したのは、バラモン教の王朝で北インドを統一し、西暦320年から550年頃まで栄えたグプタ朝においてである。Āryabhaṭa(アリヤバータ)の数学、天文学の著書は11世紀のアラビアの歴史家al-Bīrūnī〔アルベルニ、973~1048年、ホラズム出身の著述家、数学者、天文学者、旅行家、哲学者、薬学者、占星学者でもある〕によって研究された。al-Bīrūnī(アルベルニ)の研究によれば、同名の二人の数学者がおり、年長のĀryabhaṭa(アーリヤバタ)が天文学、数学の優れた著作を残したとされるが、近年の研究では同一人物とする説もある。
Āryabhaṭa(アリヤバータ)が活動したのは、バラモン教の王朝で北インドを統一し、西暦320年から550年頃まで栄えたグプタ朝においてである。Āryabhaṭa(アリヤバータ)の数学、天文学の著書は11世紀のアラビアの歴史家al-Bīrūnī〔アルベルニ、973~1048年、ホラズム出身の著述家、数学者、天文学者、旅行家、哲学者、薬学者、占星学者でもある〕によって研究された。al-Bīrūnī(アルベルニ)の研究によれば、同名の二人の数学者がおり、年長のĀryabhaṭa(アーリヤバタ)が天文学、数学の優れた著作を残したとされるが、近年の研究では同一人物とする説もある。
現在のビハール州のパトナに近いクスマプラで、天文学書『Aryabhatiya(アーリヤバティーヤ)』を著したとされる。この3章には、カリ・ユガ暦の3600年に23歳でこれを書いたという記述がある。
※Yuga(ユガ)暦:Yuga (ユガ)は、インド哲学において、循環する4つの時期からなる「時代」の名前である。4つの時期とはサティヤ・ユガ、トレーター・ユガ、ドヴァーパラ・ユガ、そして最後にカリ・ユガである。それぞれの期間においては、法や徳、知恵、知識、知力、寿命、感情や肉体の強さが徐々に低下していくというものという。
1.Satya Yuga(サティヤ・ユガ) - 徳が支配する時代であり、人間の平均身長は21〔キュービット、Ⅰcubitは「肘から中指の先端までの長さで 0.4572 m」、平均寿命は400年になる。
2.Treta Yuga(トレーター・ユガ) - 徳が4分の3、罪が4分の1を占める。人間の平均身長は14キュービット、平均寿命は300年になる。
3.Dvapara(ドヴァーパラ・ユガ) - 徳が2分の1、罪が2分の1を占める。人間の平均身長は7キュービット、平均寿命は200年になる。
4.Kali Yuga(カリ・ユガ) - 徳が4分の1、罪が4分の3を占める。人間の平均身長は3.5キュービット、平均寿命は100年になる。
彼の最も有名な著作が『Aryabhatiya(アーリヤバティーヤ)』で、革命的な数学の知識ばかりでなく、地動説にたつ宇宙モデルや、測地学の結果が含まれている。正弦の最初の三角法表を作成し、代数学、無限小、微分方程式の解法とアルゴリズムを開発し、現代と同等な手法により線型方程式の解を求めた。万有引力の地動説に基づく太陽中心の宇宙モデルとして、惑星が楕円軌道をもつことを述べている。
『Aryabhatiya(アーリヤバティーヤ)』はサンスクリット語で書かれた123連の韻文からなる。Āryabhaṭa(アリヤバータ)の著書に記されている知識には以下のものが含まれる。
・円周率の近似値を π≒62832/20000=3.1416 とした。これは小数点以下4桁まであっている近似値である。ただし、これらの値に到達した方法は記されていない。
・三角関数の求め方と簡単な表
・地球の自転周期と月の公転周期の比を27.27,3964と求める。これは恒星月の約27.32日に近い。
Āryabhaṭa(アリヤバータ)の研究は、Varahamihira〔ヴァラーハミヒラ、505~587年、古代インドの天文学者、占星術師〕やBhāskaraⅠ世〔バースカラ、7世紀の人物〕、Kerala(ケーララ)学派(インドのケーララ地方で活動した数学と天文学の学派)など後世の研究者たちに影響を与えたという。
現在のビハール州のパトナに近いクスマプラで、天文学書『Aryabhatiya(アーリヤバティーヤ)』を著したとされる。この3章には、カリ・ユガ暦の3600年に23歳でこれを書いたという記述がある。
※Yuga(ユガ)暦:Yuga (ユガ)は、インド哲学において、循環する4つの時期からなる「時代」の名前である。4つの時期とはサティヤ・ユガ、トレーター・ユガ、ドヴァーパラ・ユガ、そして最後にカリ・ユガである。それぞれの期間においては、法や徳、知恵、知識、知力、寿命、感情や肉体の強さが徐々に低下していくというものという。
1.Satya Yuga(サティヤ・ユガ) - 徳が支配する時代であり、人間の平均身長は21〔キュービット、Ⅰcubitは「肘から中指の先端までの長さで 0.4572 m」、平均寿命は400年になる。
2.Treta Yuga(トレーター・ユガ) - 徳が4分の3、罪が4分の1を占める。人間の平均身長は14キュービット、平均寿命は300年になる。
3.Dvapara(ドヴァーパラ・ユガ) - 徳が2分の1、罪が2分の1を占める。人間の平均身長は7キュービット、平均寿命は200年になる。
4.Kali Yuga(カリ・ユガ) - 徳が4分の1、罪が4分の3を占める。人間の平均身長は3.5キュービット、平均寿命は100年になる。
彼の最も有名な著作が『Aryabhatiya(アーリヤバティーヤ)』で、革命的な数学の知識ばかりでなく、地動説にたつ宇宙モデルや、測地学の結果が含まれている。正弦の最初の三角法表を作成し、代数学、無限小、微分方程式の解法とアルゴリズムを開発し、現代と同等な手法により線型方程式の解を求めた。万有引力の地動説に基づく太陽中心の宇宙モデルとして、惑星が楕円軌道をもつことを述べている。
『Aryabhatiya(アーリヤバティーヤ)』はサンスクリット語で書かれた123連の韻文からなる。Āryabhaṭa(アリヤバータ)の著書に記されている知識には以下のものが含まれる。
・円周率の近似値を π≒62832/20000=3.1416 とした。これは小数点以下4桁まであっている近似値である。ただし、これらの値に到達した方法は記されていない。
・三角関数の求め方と簡単な表
・地球の自転周期と月の公転周期の比を27.27,3964と求める。これは恒星月の約27.32日に近い。
Āryabhaṭa(アリヤバータ)の研究は、Varahamihira〔ヴァラーハミヒラ、505~587年、古代インドの天文学者、占星術師〕やBhāskaraⅠ世〔バースカラ、7世紀の人物〕、Kerala(ケーララ)学派(インドのケーララ地方で活動した数学と天文学の学派)など後世の研究者たちに影響を与えたという。
2次方程式は、エジプトやバビロニアの記録に断片的に現われているが、これを初めて本格的にとりあかったのは、前にも述べたようにHeron(ヘロン)であろうという。Deophantos(ディオファントス)もまた、2次方程式を取り扱ったことはすでに述べた。
しかし、いずれの場合にも負の数の観念はまだ存在せず、したがって、2次方程式に2つの解があることは認められていなかった。
 正の数、0、負の数の概念を確立し、2次方程式には2つの解がありうることを初めてはっきりと認めたのはインドの人たちである。Āryabhaṭ a(アリヤバータ、476~550年頃〕、Brahmagupta(ブラーマグプタ、598~668年?)、Bhāskara(バースカラ、1114~1185年)は、2次方程式をもっとも一般的な形で取り扱っている。(左図参照)
正の数、0、負の数の概念を確立し、2次方程式には2つの解がありうることを初めてはっきりと認めたのはインドの人たちである。Āryabhaṭ a(アリヤバータ、476~550年頃〕、Brahmagupta(ブラーマグプタ、598~668年?)、Bhāskara(バースカラ、1114~1185年)は、2次方程式をもっとも一般的な形で取り扱っている。(左図参照)
これは現在の2次方程式の解き方と全く同じである。Āryabhaṭ a(アリヤバータ)とBrahmagupta(ブラーマグプタ)は、ときには正の解、またときには負の解を採用するということをしている。
これに対して、2次方程式をこの方法で解き、2次方程式には2つの解がありうることをはっきりと認めたのは Bhāskara(バースカラ)である。彼は次のようにいっている。
「正の数の平方も、負の数の平方も正の数である。したがって、正の数の平方根は2つあって、その一方は正の数、他の数は負の数である。しかし、負の数の平方根は存在しない。なぜなら、負の数は絶対にある数の平方にはなりえないからである」
しかし、いずれの場合にも負の数の観念はまだ存在せず、したがって、2次方程式に2つの解があることは認められていなかった。
これは現在の2次方程式の解き方と全く同じである。Āryabhaṭ a(アリヤバータ)とBrahmagupta(ブラーマグプタ)は、ときには正の解、またときには負の解を採用するということをしている。
これに対して、2次方程式をこの方法で解き、2次方程式には2つの解がありうることをはっきりと認めたのは Bhāskara(バースカラ)である。彼は次のようにいっている。
「正の数の平方も、負の数の平方も正の数である。したがって、正の数の平方根は2つあって、その一方は正の数、他の数は負の数である。しかし、負の数の平方根は存在しない。なぜなら、負の数は絶対にある数の平方にはなりえないからである」
プロフィール
ハンドルネーム:
目高 拙痴无
年齢:
93
誕生日:
1932/02/04
自己紹介:
くたばりかけの糞爺々です。よろしく。メールも頼むね。
sechin@nethome.ne.jp です。
sechin@nethome.ne.jp です。
カレンダー
| 12 | 2026/01 | 02 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
最新コメント
[enken 02/23]
[中村東樹 02/04]
[m、m 02/04]
[爺の姪 01/13]
[レンマ学(メタ数学) 01/02]
[m.m 10/12]
[爺の姪 10/01]
[あは♡ 09/20]
[Mr.サタン 09/20]
[Mr.サタン 09/20]
最新トラックバック
ブログ内検索
カウンター
