瘋癲爺 拙痴无の戯言・放言・歯軋り
古代中国の数学書に「九章算術(きゅうしょうさんじゅつ)」というのがある。
 九章からなるいわゆる問題集形式の数学書で、著者は判っておらず、加筆修正を経て次第に現在に伝わる形に完成したとされている。研究によると前漢の張蒼(ちょう そう、?~BC152年)や耿寿昌(前漢、生卒年不詳)も加筆したことがわかっている。263年に劉徽の註釈本を制作していたことなどから、制作年代はBC1世紀からBC2世紀頃であると考えられている。
九章からなるいわゆる問題集形式の数学書で、著者は判っておらず、加筆修正を経て次第に現在に伝わる形に完成したとされている。研究によると前漢の張蒼(ちょう そう、?~BC152年)や耿寿昌(前漢、生卒年不詳)も加筆したことがわかっている。263年に劉徽の註釈本を制作していたことなどから、制作年代はBC1世紀からBC2世紀頃であると考えられている。
延べ246問が九章からなる構成でできていることに由来する。
1) 方田 - 主に田畑の(年貢のための)面積計算と分数の計算。(38問)
2) 粟米 - 交換比率の異なる商品を物々交換するための計算。比例算。(46問)
3) 衰分(さぶん) - 商品とお金との分配。比例按分。利息計算。(20問)
4) 少広 - 面積体積から辺の長さを求める。平方根や立方根。(24問)
5) 商功 - 土石の量などを求める土木計算。体積。 (28問)
6) 均輸 - 租税の計算。複雑な比例問題。 (28問)
7) 盈不足 - 鶴亀算。復仮定法。(20問)
8) 方程 - 連立一次方程式の解法。また、その為の負の数とその演算規則の導入。 (18問)
9) 句股 - ピタゴラスの定理に関する問題。測量など。(24問)
九章算術には周以来の古代中国の数学問題と、漢の時代の最新の数学問題が収められている。九章算術は内容の量と質の良さから古代中国の中心的な算書として用いられ、古代中国の数学史において数学体系を完成させた本であるとされている。九章算術で完成された数学のスタイルの影響は清の中期頃の西洋数学が入って来るまで続いた。現代中国においても算数の教科書のコラムで九章算術の記述に言及している。
九章算術は問題を出し答えと計算法を出す帰納的なアプローチである。具体的には問題の記述の後、「答曰く、」ではじまる答えと、「術曰く、」ではじまる計算式(時には問題の解法としての役も得る)の記述という具合である。演繹的な手法のヨーロッパ・アラブ数学とは異なり、中国の以後の数学書はこの記述方法を採った。 このスタイルは日本にも輸入され、和算の書籍や算額なども「答曰く、」や「術曰く、」を含む形で書かれている。
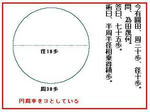 例) いま円田あり。周が30歩、(直)径が10歩であれば、田の広さはいくらか。 答曰く、75歩。 術に曰く、半周「ℓ/2」と半径(r)を相乗して積歩(S)を得る。という調子である。
例) いま円田あり。周が30歩、(直)径が10歩であれば、田の広さはいくらか。 答曰く、75歩。 術に曰く、半周「ℓ/2」と半径(r)を相乗して積歩(S)を得る。という調子である。
S=ℓ/2 ×r=15×5=75(歩)
方田章に見える長さの単位は尺であり、6尺が1歩、三百歩が1里。積歩は面積を表わすが、平方歩という表現はなく、長さの単位と同じく75歩とかかれる。
歴史上この本を註釈した数学者は多いが、特に劉 徽(りゅう き、三国時代の数学者、220?~280?年)による註釈本は有名である。
 例えば、九章算術の原本では円周率を3として扱っているのに対して、劉徽は左図のようであり近似値として3.14を使うのがよいと註釈をしている。これは彼の名を称えて、徽率と呼ばれた。この当時(3世紀頃)の世界における最高精度の近似であったという。
例えば、九章算術の原本では円周率を3として扱っているのに対して、劉徽は左図のようであり近似値として3.14を使うのがよいと註釈をしている。これは彼の名を称えて、徽率と呼ばれた。この当時(3世紀頃)の世界における最高精度の近似であったという。
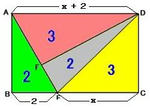 頭の体操15の解) △ABE:四角形AECE=2:(3+5)=2:8
頭の体操15の解) △ABE:四角形AECE=2:(3+5)=2:8
BE=2、EC=ⅹ とすれば、AD=2+ⅹ
△ABE:四角形AECE=BE:(EC+AD)=2:(2ⅹ+2)=2:8
内項の積と外項の積は等しいから 2(2ⅹ+2)=16
∴ ⅹ=3 従って △ABE:△DEC:△AED=2:3:5
△AFD:△DFE=AF:FE=3:2 とすればよい。
延べ246問が九章からなる構成でできていることに由来する。
1) 方田 - 主に田畑の(年貢のための)面積計算と分数の計算。(38問)
2) 粟米 - 交換比率の異なる商品を物々交換するための計算。比例算。(46問)
3) 衰分(さぶん) - 商品とお金との分配。比例按分。利息計算。(20問)
4) 少広 - 面積体積から辺の長さを求める。平方根や立方根。(24問)
5) 商功 - 土石の量などを求める土木計算。体積。 (28問)
6) 均輸 - 租税の計算。複雑な比例問題。 (28問)
7) 盈不足 - 鶴亀算。復仮定法。(20問)
8) 方程 - 連立一次方程式の解法。また、その為の負の数とその演算規則の導入。 (18問)
9) 句股 - ピタゴラスの定理に関する問題。測量など。(24問)
九章算術には周以来の古代中国の数学問題と、漢の時代の最新の数学問題が収められている。九章算術は内容の量と質の良さから古代中国の中心的な算書として用いられ、古代中国の数学史において数学体系を完成させた本であるとされている。九章算術で完成された数学のスタイルの影響は清の中期頃の西洋数学が入って来るまで続いた。現代中国においても算数の教科書のコラムで九章算術の記述に言及している。
九章算術は問題を出し答えと計算法を出す帰納的なアプローチである。具体的には問題の記述の後、「答曰く、」ではじまる答えと、「術曰く、」ではじまる計算式(時には問題の解法としての役も得る)の記述という具合である。演繹的な手法のヨーロッパ・アラブ数学とは異なり、中国の以後の数学書はこの記述方法を採った。 このスタイルは日本にも輸入され、和算の書籍や算額なども「答曰く、」や「術曰く、」を含む形で書かれている。
S=ℓ/2 ×r=15×5=75(歩)
方田章に見える長さの単位は尺であり、6尺が1歩、三百歩が1里。積歩は面積を表わすが、平方歩という表現はなく、長さの単位と同じく75歩とかかれる。
歴史上この本を註釈した数学者は多いが、特に劉 徽(りゅう き、三国時代の数学者、220?~280?年)による註釈本は有名である。
BE=2、EC=ⅹ とすれば、AD=2+ⅹ
△ABE:四角形AECE=BE:(EC+AD)=2:(2ⅹ+2)=2:8
内項の積と外項の積は等しいから 2(2ⅹ+2)=16
∴ ⅹ=3 従って △ABE:△DEC:△AED=2:3:5
△AFD:△DFE=AF:FE=3:2 とすればよい。
PR
この記事にコメントする
プロフィール
ハンドルネーム:
目高 拙痴无
年齢:
93
誕生日:
1932/02/04
自己紹介:
くたばりかけの糞爺々です。よろしく。メールも頼むね。
sechin@nethome.ne.jp です。
sechin@nethome.ne.jp です。
カレンダー
| 10 | 2025/11 | 12 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
最新コメント
[enken 02/23]
[中村東樹 02/04]
[m、m 02/04]
[爺の姪 01/13]
[レンマ学(メタ数学) 01/02]
[m.m 10/12]
[爺の姪 10/01]
[あは♡ 09/20]
[Mr.サタン 09/20]
[Mr.サタン 09/20]
最新トラックバック
ブログ内検索
カウンター
