瘋癲爺 拙痴无の戯言・放言・歯軋り
小さな王国でのことである。6個の連隊(A、B、C、D、E、F)から6階級の士官(大佐、中佐、少佐、大尉、中尉、少尉)を1名ずつ呼び集めて、36人を各列6人ずつの6列縦隊に整列させる。この正方形の隊列は方陣をなすが、縦に見ても横に見ても、同じ連隊の士官、又同じ階級の士官が一線に並ぶことがないようにすることが出来るかどうか? というパズル的問題である。Euler自身はその様な配列の不可能なことを感じ取っていたようである。
ここで数6を一般のnで置き換えた問題を取り上げると、n種類の記号A₁、A₂、……、An および他のn種類の記号a₁、a₂、……an が与えられたとして、Aiaj の形の組み合わせn²個をn行n列の正方形に配列して、各行各列において、第1成分Aiにも、第2成分ajにも重複が起こらないようにしたものを「n次オイラー方陣」と名付ける。
すぐに確かめられるように、2次オイラー方陣は存在しない。6次のオイラー方陣が上に述べた「士官36人の問題」に当たる。
Eulerは1782年に n=2、6、10、14…、 すなわち n=4m+2 の形の場合に、オイラー方陣は存在しないとする推測を発表した。Eulerの権威のために長い間、広くそのように信じられてきた。
ここでこの3次の魔法陣の各数から1を引いて0から8までの数に直し、さらに三進法で、00、01、……、22で表わせば、3次のオイラー方陣になる。(左図参照)
PR
枕橋から墨田区役所前を通り、吾妻橋を渡ると、隅田公園の花川戸遊歩道を北上。公園内は流鏑馬の準備で道に白砂が敷かれているので、途中からテラスにおりて、言問橋下、桜橋下を通り、水上バス桜橋乗り場の昇降口から山谷堀水門広場を横切って帰宅した。
昨日の夕刊に大きくボストンマラソンでテロらしき爆発があったというので、ウェブニュースを探してみた。
今朝のウェブニュースから
 隋の煬帝の墓 中国の江蘇省で発見か ―― 中国東部の江蘇省で、都市開発の工事の際に偶然、1400年前に大運河を築いたことなどで知られる隋王朝の煬帝のものとみられる墓が見つかったと、地元の当局が発表しました。/中国国営の新華社通信などによりますと、墓が見つかったのは江蘇省揚州の郊外で、都市開発の建設工事の際に偶然、面積が30平方メートルほどの古代のれんがでできた石室2つが見つかりました。/地元の文化財当局が調査したところ、石室のうち1つから「隋の煬帝」と書かれた墓誌のほか、銅製の工芸品や玉がちりばめられた金のベルトなどの副葬品が発掘されました。/盗掘の跡があり、人骨などは見つかっていませんが、地元当局は、発掘された副葬品は高貴な人物にしか見られないことなどから、墓の主は隋の第二代皇帝、煬帝と基本的に認定できると発表しました。/煬帝は中国の南北を縦断する大運河を築いたほか、聖徳太子が当時の中国を日本と対等にみて「日出づる処の天子」で始まる手紙を書いたことに激怒したことなどで知られています。/江蘇省揚州には、別に煬帝の墓とされる陵墓がありますが、歴史の資料に煬帝の墓は何度も移されていると書かれていることから、地元当局は今後、今回発見された墓との関係を詳しく調べることにしています。 〔NHK NEWS WEB 4月15日 22時59分〕
隋の煬帝の墓 中国の江蘇省で発見か ―― 中国東部の江蘇省で、都市開発の工事の際に偶然、1400年前に大運河を築いたことなどで知られる隋王朝の煬帝のものとみられる墓が見つかったと、地元の当局が発表しました。/中国国営の新華社通信などによりますと、墓が見つかったのは江蘇省揚州の郊外で、都市開発の建設工事の際に偶然、面積が30平方メートルほどの古代のれんがでできた石室2つが見つかりました。/地元の文化財当局が調査したところ、石室のうち1つから「隋の煬帝」と書かれた墓誌のほか、銅製の工芸品や玉がちりばめられた金のベルトなどの副葬品が発掘されました。/盗掘の跡があり、人骨などは見つかっていませんが、地元当局は、発掘された副葬品は高貴な人物にしか見られないことなどから、墓の主は隋の第二代皇帝、煬帝と基本的に認定できると発表しました。/煬帝は中国の南北を縦断する大運河を築いたほか、聖徳太子が当時の中国を日本と対等にみて「日出づる処の天子」で始まる手紙を書いたことに激怒したことなどで知られています。/江蘇省揚州には、別に煬帝の墓とされる陵墓がありますが、歴史の資料に煬帝の墓は何度も移されていると書かれていることから、地元当局は今後、今回発見された墓との関係を詳しく調べることにしています。 〔NHK NEWS WEB 4月15日 22時59分〕
昨日のブログ「仁科の津波」の記事にある2神社について、調べてみた。
 佐波神社 賀茂郡西伊豆町仁科 東経138度46分25.27秒、北緯34度46分23.63秒に鎮座。
佐波神社 賀茂郡西伊豆町仁科 東経138度46分25.27秒、北緯34度46分23.63秒に鎮座。
この神社は西伊豆町役場の北西約800m、136号線の信号から少し東へ入ったところに鎮座まします。沢田コミュニティ防災センターに隣接して、参道入口には明神鳥居や「佐波神社」と刻まれた社号標も建っている。鳥居を潜り、コミュニティ防災センター前を通ると左に手水舎があり、神池に架かる神橋を渡ると境内入口には両部鳥居が建つ。大きな境内には招魂社が祀られ、参道正面奥には拝殿が建ち、拝殿内の二つの額には「八幡宮」「三島宮」と社名があり、この社が、八幡宮と三島宮の2社が同座している神社だとわかる。拝殿後方に本殿鞘堂があり、その本殿の後方には大きな岩の下に祭祀場がある。又、末社も多数祀られているという。
御祭神:積羽八重事代主命、廣幡八幡大神
祭礼日:11月2・3日 人形三番叟の奉納(昭和四十七年三月 県指定 無形民俗文化財)
境内社:招魂社他
由緒:「延喜式内社」としての「神明帳」に登録されて年代も古く由緒ある神社であり、伊豆神明帳に佐波神社従四位上「志での明神」「にいの明神」二座、佐波は地名であり澤である。
八幡宮については「神宮皇后三韓を征し給う時、初めてこの地に祀る。仁科の荘、総社八幡旧那賀郡十七ケ村の総鎮守也、五百年前迄は海辺にありしに、海溢〔かいいつ、津波〕にて今の地に止まる。依て三島明神と祠を並べて立つ」とあり、一方三島明神は地主神であり古老の口碑、社伝として「一蜘子葦ノ葉ニ乗リ、鴨ケ池ヲ渡ヲ診テ始メテ船ヲ此ノ地に造ル。人皇十一代崇神天皇ノ御座船ヲ鴨ケ池ノ辺リニ造ルト、天皇ヨリ三島神ノ神体ヲ賜リ其造船ノ地ニ祀祭ス、是レヲ佐波神社トス」と記載されている。
三島宮・八幡宮はそれぞれ別殿に鎮座されていて、二社が鴨ケ池より現社地に奉遷し造営されたのは棟札「奉祈造立一字八幡大菩薩」「奉祈造立一字三島大明神」から見ると慶長14(1609)年である。
また、いつ一社に合祀されたのかを棟札から見ると文政6(1823)年3月である。 (神社案内板より)
 金比羅宮 賀茂郡西伊豆町仁科 東経138度46分30.69秒、北緯34度46分02.13秒に鎮座。
金比羅宮 賀茂郡西伊豆町仁科 東経138度46分30.69秒、北緯34度46分02.13秒に鎮座。
この神社は136号線・仁科東信号から約150m程南に向かうと、右側安城温泉浴場右に参道入口がある、極小さな社地の神社ですが崇敬される方は大事に守っていらっしゃるようである。
御祭神:大物主命、毘沙門天、崇徳天皇、塩椎大明神
祭礼日:4月10日
由緒:この社は文政年間(1818~1829)に大物主命、毘沙門天、崇徳天皇の三柱を御祭神として創建され、文政11年(1828)には宮城県塩釜市の塩釜神社から塩椎大明神も分霊勧請された。社殿内には江戸時代の弁財船(北前船)や日露戦争の武運長久、病気平癒、賭博と禁酒、安産祈願などの数々の絵馬が奉納され、地域区民や特に舟入水主の尊信は最も深く、今も多くの人々が参詣しているという。
昨日のブログ「仁科の津波」の記事にある2神社について、調べてみた。
この神社は西伊豆町役場の北西約800m、136号線の信号から少し東へ入ったところに鎮座まします。沢田コミュニティ防災センターに隣接して、参道入口には明神鳥居や「佐波神社」と刻まれた社号標も建っている。鳥居を潜り、コミュニティ防災センター前を通ると左に手水舎があり、神池に架かる神橋を渡ると境内入口には両部鳥居が建つ。大きな境内には招魂社が祀られ、参道正面奥には拝殿が建ち、拝殿内の二つの額には「八幡宮」「三島宮」と社名があり、この社が、八幡宮と三島宮の2社が同座している神社だとわかる。拝殿後方に本殿鞘堂があり、その本殿の後方には大きな岩の下に祭祀場がある。又、末社も多数祀られているという。
御祭神:積羽八重事代主命、廣幡八幡大神
祭礼日:11月2・3日 人形三番叟の奉納(昭和四十七年三月 県指定 無形民俗文化財)
境内社:招魂社他
由緒:「延喜式内社」としての「神明帳」に登録されて年代も古く由緒ある神社であり、伊豆神明帳に佐波神社従四位上「志での明神」「にいの明神」二座、佐波は地名であり澤である。
八幡宮については「神宮皇后三韓を征し給う時、初めてこの地に祀る。仁科の荘、総社八幡旧那賀郡十七ケ村の総鎮守也、五百年前迄は海辺にありしに、海溢〔かいいつ、津波〕にて今の地に止まる。依て三島明神と祠を並べて立つ」とあり、一方三島明神は地主神であり古老の口碑、社伝として「一蜘子葦ノ葉ニ乗リ、鴨ケ池ヲ渡ヲ診テ始メテ船ヲ此ノ地に造ル。人皇十一代崇神天皇ノ御座船ヲ鴨ケ池ノ辺リニ造ルト、天皇ヨリ三島神ノ神体ヲ賜リ其造船ノ地ニ祀祭ス、是レヲ佐波神社トス」と記載されている。
三島宮・八幡宮はそれぞれ別殿に鎮座されていて、二社が鴨ケ池より現社地に奉遷し造営されたのは棟札「奉祈造立一字八幡大菩薩」「奉祈造立一字三島大明神」から見ると慶長14(1609)年である。
また、いつ一社に合祀されたのかを棟札から見ると文政6(1823)年3月である。 (神社案内板より)
この神社は136号線・仁科東信号から約150m程南に向かうと、右側安城温泉浴場右に参道入口がある、極小さな社地の神社ですが崇敬される方は大事に守っていらっしゃるようである。
御祭神:大物主命、毘沙門天、崇徳天皇、塩椎大明神
祭礼日:4月10日
由緒:この社は文政年間(1818~1829)に大物主命、毘沙門天、崇徳天皇の三柱を御祭神として創建され、文政11年(1828)には宮城県塩釜市の塩釜神社から塩椎大明神も分霊勧請された。社殿内には江戸時代の弁財船(北前船)や日露戦争の武運長久、病気平癒、賭博と禁酒、安産祈願などの数々の絵馬が奉納され、地域区民や特に舟入水主の尊信は最も深く、今も多くの人々が参詣しているという。
因みに、兼愛塾臨海学校の宿舎 長松寺から築地橋に出る途中にあった神社は「築地神明神社(賀茂郡西伊豆町仁科651)」といい、本殿は1779(安永8)年に建立された 神明造 こけら葺 の建物である。
昨日のブログの伊豆半島の仁科の佐波神社に残る棟札に地震の記録の記事が少々気になったので調べてみた。以下、インターネットで「1707年宝永地震震源域の東端位置」という論文から借用した。
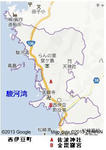 宝永四年十月四日(1707年10月28日)の東海一南海地震は日本史上最大規模の地震と考えられている。嘉永七年十一月四日、五日〔1854年12月23日、 24日〕の東海、南海地震はこの順に約32時間の間隔をおいて別々に発生した。宝永東海一南海地震では東海地震と南海地震がほぼ同時に発生した〔白鳳〕地震以来1944年、 1946年〔昭和〕まで9回、東海,南海地震が90年から262年の間隔をおいて発生したことが知られている。その発生間隔および震源過程は複雑である。
宝永四年十月四日(1707年10月28日)の東海一南海地震は日本史上最大規模の地震と考えられている。嘉永七年十一月四日、五日〔1854年12月23日、 24日〕の東海、南海地震はこの順に約32時間の間隔をおいて別々に発生した。宝永東海一南海地震では東海地震と南海地震がほぼ同時に発生した〔白鳳〕地震以来1944年、 1946年〔昭和〕まで9回、東海,南海地震が90年から262年の間隔をおいて発生したことが知られている。その発生間隔および震源過程は複雑である。
宝永四年地震震源域の東端位置はこれまでにも学者の間で議論されているが、この東端位置についての問題はいまだ未解決のように思われる。原因として、伊豆半島西岸での地震史料調査が不十分で、あることが挙げられる。宝永四年地震震源域の東端位置を決定することを目的として,伊豆半島西岸の宝永四年地震および嘉永七年地震に関する地震史料の調査を行った。この地域の神社・寺院に保存されている棟札銘文を主に調査した。この調査結果をこれまでの研究による駿河湾周辺の震度分布および地殻変動と比較して、宝永四年地震震源域の東端位置を推定する。
 静岡県賀茂郡西伊豆町:左記のTable 1に西伊豆町の2神社に所蔵きれている棟札の銘文を示す。
静岡県賀茂郡西伊豆町:左記のTable 1に西伊豆町の2神社に所蔵きれている棟札の銘文を示す。
史料1(八幡社(佐波神社内))は享保2(1717)年に書かれた。 14年前、つまり元禄16(1703)年11月23日の未明に発生した元禄地震による地震動と津波が西伊豆仁科を襲ったこと、そして同じ伊豆の下回は更に大きな被害を被ったことを示唆している。宝永四年地震は宝永4(1707」年10月4日未刻(午後2時)に発生した.宝永四年地震は元禄地震から4年後、史料1が書かれた享保2年の10年前に発生した。従って八幡宮宝殿所を建立しこの棟札を奉納した人々は、もし仁科が宝永四年地震による地震動・津波により大きな被害を被っていたならば、当然この棟札銘文にそのことを書いていたはずである。しかし、宝永四年地震についての記載はない。
史料2 (金毘羅社)は安政五年(1858) に書かれた.嘉永七年十一月四日朝五ッ時(午前8時)の大地震により地が欠け、山が崩れ、大i章波が発生したことが書かれている。低位の平地に津波が何回も押し寄せ、田子村にて波高4.5~5m、 250戸水漬け、中には流失した家屋もある。仁科正円で波高3m、軒並浸水し仁科川を遡り、浜から2kmの寺川の田畑や住家まで流し込んで、いる。 また同じ伊豆の下回では人家が残らず流失し大きな被害が出たことも史料2には書かれている。
宝永四年地震震源域の東端位置はこれまでにも学者の間で議論されているが、この東端位置についての問題はいまだ未解決のように思われる。原因として、伊豆半島西岸での地震史料調査が不十分で、あることが挙げられる。宝永四年地震震源域の東端位置を決定することを目的として,伊豆半島西岸の宝永四年地震および嘉永七年地震に関する地震史料の調査を行った。この地域の神社・寺院に保存されている棟札銘文を主に調査した。この調査結果をこれまでの研究による駿河湾周辺の震度分布および地殻変動と比較して、宝永四年地震震源域の東端位置を推定する。
史料1(八幡社(佐波神社内))は享保2(1717)年に書かれた。 14年前、つまり元禄16(1703)年11月23日の未明に発生した元禄地震による地震動と津波が西伊豆仁科を襲ったこと、そして同じ伊豆の下回は更に大きな被害を被ったことを示唆している。宝永四年地震は宝永4(1707」年10月4日未刻(午後2時)に発生した.宝永四年地震は元禄地震から4年後、史料1が書かれた享保2年の10年前に発生した。従って八幡宮宝殿所を建立しこの棟札を奉納した人々は、もし仁科が宝永四年地震による地震動・津波により大きな被害を被っていたならば、当然この棟札銘文にそのことを書いていたはずである。しかし、宝永四年地震についての記載はない。
史料2 (金毘羅社)は安政五年(1858) に書かれた.嘉永七年十一月四日朝五ッ時(午前8時)の大地震により地が欠け、山が崩れ、大i章波が発生したことが書かれている。低位の平地に津波が何回も押し寄せ、田子村にて波高4.5~5m、 250戸水漬け、中には流失した家屋もある。仁科正円で波高3m、軒並浸水し仁科川を遡り、浜から2kmの寺川の田畑や住家まで流し込んで、いる。 また同じ伊豆の下回では人家が残らず流失し大きな被害が出たことも史料2には書かれている。
昨日の早朝関西でかなり大きな地震があったらしい。ウェブニュースに拠れば、以下の通り。
 淡路島の住宅被害など 500棟超す ―― 13日朝早く、兵庫県淡路市で、震度6弱の激しい揺れを観測する地震がありました。/この地震で、兵庫県の淡路島の3つの市は、被害を受けた住宅の調査を行った結果、淡路島では、これまでに500棟を超える建物で被害が出ています。/このうち、洲本市では、午前中から、職員が市内すべての住宅などを対象に被害状況を調査し、これまでに118棟の住宅の一部が損壊したほか、空き屋など住宅以外の建物も27棟で被害が出ています。/また、淡路市では、午後6時現在、住宅など385棟が壊れたということです。/さらに、南あわじ市では、午後5時現在、住宅2棟が半壊、12棟が一部損壊しているのが確認されたということです。 〔NHK NEWS WEB 4月13日 18時55分〕
淡路島の住宅被害など 500棟超す ―― 13日朝早く、兵庫県淡路市で、震度6弱の激しい揺れを観測する地震がありました。/この地震で、兵庫県の淡路島の3つの市は、被害を受けた住宅の調査を行った結果、淡路島では、これまでに500棟を超える建物で被害が出ています。/このうち、洲本市では、午前中から、職員が市内すべての住宅などを対象に被害状況を調査し、これまでに118棟の住宅の一部が損壊したほか、空き屋など住宅以外の建物も27棟で被害が出ています。/また、淡路市では、午後6時現在、住宅など385棟が壊れたということです。/さらに、南あわじ市では、午後5時現在、住宅2棟が半壊、12棟が一部損壊しているのが確認されたということです。 〔NHK NEWS WEB 4月13日 18時55分〕
早朝の地震、官邸も国交省も「ミサイル発射か」 ―― 13日午前5時33分ごろ、兵庫県の淡路島で震度6弱を記録するなど、近畿、中四国を中心に広範囲で地震があり、警察庁によると5府県で計23人が重軽傷を負った。関西の震度6以上の地震は1995年の阪神大震災以来。気象庁によると震源は淡路島付近で、深さは約15キロ。マグニチュード「M」6.3と推定され、津波はなかった。一方、国土交通省は、地震を受け大阪航空局(大阪市)が、空港などに被害状況報告を求めるメールを送る際「北朝鮮からミサイルが発射された」と誤報を送ったと発表した。
13日の地震をめぐっては、北朝鮮のミサイル発射誤報騒動があった。/国交省によると、地震発生直後、大阪航空局で危機管理を担当する男性係長(46)が「北朝鮮からミサイルが発射されました。状況確認と報告を願います」という内容のメールを、西日本の空港やレーダー施設など計87ヵ所に誤送信した。/係長は公用の携帯電話から、地震の被害状況等の報告要請メールを送る操作をしていた。携帯内には勤務時間外のミサイル発射に備え、メールを宛先まで入力し保存していた。誤操作で、これが送られたとみられる。/約6分後に取り消しメールを送ったが、北九州空港では午前5時半発のスターフライヤー便が、管制官の指示で離陸を見合わせ、3~4分遅れた。11日にも、同省の航空交通管理センター(福岡市)が、全国の航空管制施設など計59ヵ所にミサイル発射と誤発信していた。ミスの連続を受け政府高官は、同省幹部らを処分する方向で検討に入った。
一方、首相官邸はこの日、地震とミサイルの危機管理の両面対応に追われた。菅義偉官房長官は13日早朝、非常用電話で地震発生の連絡を受けた際、とっさに「北朝鮮のミサイル発射かな」と受け止めたという。この日、首相が都内の私邸から外出したのは、地震の緊張状態が落ち着いた午後になってから。政府筋は初動の順調さを強調したが、与党幹部は「同時にミサイルも発射されていたら、うまく処理できたかは分からない」と指摘した。 (2013年4月14日06時04分 スポーツ報知)
昨日の朝、姪のchisatoから携帯にメールが入った。
2013年4月13日、09:37 発信 朝早く、びっくりしましたが、無事ですので〓。日本中、どこにいても油断してはいけないということですね。では。 〓from chisato〓
午後、姪と電話で話したが、今朝の朝日新聞土曜版に、爺たちが毎年臨海学校をやっていた伊豆半島の仁科の佐波神社に残る棟札に地震の記録が書かれた興味深い記事が載っているということで早速調べてみた。
歴史学者磯田道史氏が書いている歴史コラムだ。奇しくも地震の記事である。曰く、
 ……400年前に願栄という僧侶が伊豆半島にいた。私は無名のこの僧侶に感謝してもしきれない。というのもこの願栄は後世の人間を津波から護る「重要な記述」を気の板に書いて残してくれた。/慶長9年の暮れ(1605年2月にあたる))、伊豆半島を南海トラフ地震と大津波が襲った。/佐波神社と言う神社が年明けて再建された時、記念の棟札に、この願栄という僧侶が大変重要なことを書いた。原文を現代語訳する。/「戊午(1498)年の津波は寺川の大堰まで。その後99年申辰年12月16日(1605)は垣の内の横縄手まで津波が入った。末世にその心得がありますように。」/願栄は津波による里人の死が悔しかったに違いない。1498年の明応津波と1605年の慶長津波の浸水がどこまで来たかを後世のために書き残したのである。さらに幕末明治になって萩原正平という国学者がこの棟札を記述を元に現地踏査し津波が田園を水に浸しつつ遡った距離を割り出した(『増刷豆州志稿』)。その結果、明応津波は海から2キロ地点(津波学者の郡司嘉宣氏によれば、標高約10㍍)まできたことがわかった。これは重要な情報である。明応津波はおそらく10㍍を高さがあり、仁科の里を2㌔内陸まで浸水させている。1.4㌔浸水させた慶長津波よりもおそらく巨大だったことがわかる。ちなみに安政津波はこの付近で波髙5㍍前後とされ現在の地形でいえば1㌔程度内陸(標高4.5㍍)まできて止まったとかんがえられる。/ゆえに二品という「地形津波計」で計った歴史上の津波の大きさは 明応>慶長>安政 の順番となる。時代によって多少地形も変わるから一概にはいえないが、我々は400年まえの願栄という僧が津波のきた地点を書き残してくれたおかげで、このような防災情報を売ることが出来るのである。
……400年前に願栄という僧侶が伊豆半島にいた。私は無名のこの僧侶に感謝してもしきれない。というのもこの願栄は後世の人間を津波から護る「重要な記述」を気の板に書いて残してくれた。/慶長9年の暮れ(1605年2月にあたる))、伊豆半島を南海トラフ地震と大津波が襲った。/佐波神社と言う神社が年明けて再建された時、記念の棟札に、この願栄という僧侶が大変重要なことを書いた。原文を現代語訳する。/「戊午(1498)年の津波は寺川の大堰まで。その後99年申辰年12月16日(1605)は垣の内の横縄手まで津波が入った。末世にその心得がありますように。」/願栄は津波による里人の死が悔しかったに違いない。1498年の明応津波と1605年の慶長津波の浸水がどこまで来たかを後世のために書き残したのである。さらに幕末明治になって萩原正平という国学者がこの棟札を記述を元に現地踏査し津波が田園を水に浸しつつ遡った距離を割り出した(『増刷豆州志稿』)。その結果、明応津波は海から2キロ地点(津波学者の郡司嘉宣氏によれば、標高約10㍍)まできたことがわかった。これは重要な情報である。明応津波はおそらく10㍍を高さがあり、仁科の里を2㌔内陸まで浸水させている。1.4㌔浸水させた慶長津波よりもおそらく巨大だったことがわかる。ちなみに安政津波はこの付近で波髙5㍍前後とされ現在の地形でいえば1㌔程度内陸(標高4.5㍍)まできて止まったとかんがえられる。/ゆえに二品という「地形津波計」で計った歴史上の津波の大きさは 明応>慶長>安政 の順番となる。時代によって多少地形も変わるから一概にはいえないが、我々は400年まえの願栄という僧が津波のきた地点を書き残してくれたおかげで、このような防災情報を売ることが出来るのである。
※秋山富南(あきやまふなん、1723~1808年、字は章、通称文蔵)が著した「豆州志稿」は、その他の多くの地誌が村落ごとに記述されるのに対し、沿革・郡郷・租税・原野・川渓・橋梁・物産・神祠・仏刹・古墳・流寓・人物といった項目別になっているが、この富南の「豆州志稿」は江戸時代に印刷・刊行されることはなかった。1888年(明治21)に伊豆長岡の国学者はぎわらしょうへい萩原正平(はぎわらしょうへい、1839~1891年)がこの増補訂正・刊行を企て、正平の死後は嗣子まさお正夫が父の遺志を引き継いで1892年から1895年にかけて『増訂豆州志稿』として印刷・版行した。
婆様がメール打ち込みの練習になるからといって、塾友のYM女史にご機嫌伺いのメールを出したという。その返信に曰く、
 2013年4月13日 17:43 発信 日高道子へ カナダに行って、オーロラを見て来ました。/今日のBS NHK 9時から、同じイエローナイフのオーロラをやります。/同時期でしたので、私が見たオーロラもやるかもしれません。ご興味があれは是非に。
2013年4月13日 17:43 発信 日高道子へ カナダに行って、オーロラを見て来ました。/今日のBS NHK 9時から、同じイエローナイフのオーロラをやります。/同時期でしたので、私が見たオーロラもやるかもしれません。ご興味があれは是非に。
早速 BS BHK 午後9時からの「大沢たかお 神秘の北極圏~光と闇の旅~」を録画しておき、今朝の隅田川の徘徊から帰宅すると、早速再生してみた。
インターネットで調べると、この放送を紹介する6組の動画があった。
http://www.nhk.or.jp/ocean/arctic/movie/
婆様はYM嬢にお礼のメールを入れたらしい。すぐに返信が届いた。曰く、
本当に空一面のオーロラは素晴らしかったです。/さらに、極寒の世界にもびっくりしました。いろんなことが初めてで、いい体験させてもらいました。すべての出来事に感謝です。
早朝の地震、官邸も国交省も「ミサイル発射か」 ―― 13日午前5時33分ごろ、兵庫県の淡路島で震度6弱を記録するなど、近畿、中四国を中心に広範囲で地震があり、警察庁によると5府県で計23人が重軽傷を負った。関西の震度6以上の地震は1995年の阪神大震災以来。気象庁によると震源は淡路島付近で、深さは約15キロ。マグニチュード「M」6.3と推定され、津波はなかった。一方、国土交通省は、地震を受け大阪航空局(大阪市)が、空港などに被害状況報告を求めるメールを送る際「北朝鮮からミサイルが発射された」と誤報を送ったと発表した。
13日の地震をめぐっては、北朝鮮のミサイル発射誤報騒動があった。/国交省によると、地震発生直後、大阪航空局で危機管理を担当する男性係長(46)が「北朝鮮からミサイルが発射されました。状況確認と報告を願います」という内容のメールを、西日本の空港やレーダー施設など計87ヵ所に誤送信した。/係長は公用の携帯電話から、地震の被害状況等の報告要請メールを送る操作をしていた。携帯内には勤務時間外のミサイル発射に備え、メールを宛先まで入力し保存していた。誤操作で、これが送られたとみられる。/約6分後に取り消しメールを送ったが、北九州空港では午前5時半発のスターフライヤー便が、管制官の指示で離陸を見合わせ、3~4分遅れた。11日にも、同省の航空交通管理センター(福岡市)が、全国の航空管制施設など計59ヵ所にミサイル発射と誤発信していた。ミスの連続を受け政府高官は、同省幹部らを処分する方向で検討に入った。
一方、首相官邸はこの日、地震とミサイルの危機管理の両面対応に追われた。菅義偉官房長官は13日早朝、非常用電話で地震発生の連絡を受けた際、とっさに「北朝鮮のミサイル発射かな」と受け止めたという。この日、首相が都内の私邸から外出したのは、地震の緊張状態が落ち着いた午後になってから。政府筋は初動の順調さを強調したが、与党幹部は「同時にミサイルも発射されていたら、うまく処理できたかは分からない」と指摘した。 (2013年4月14日06時04分 スポーツ報知)
昨日の朝、姪のchisatoから携帯にメールが入った。
2013年4月13日、09:37 発信 朝早く、びっくりしましたが、無事ですので〓。日本中、どこにいても油断してはいけないということですね。では。 〓from chisato〓
午後、姪と電話で話したが、今朝の朝日新聞土曜版に、爺たちが毎年臨海学校をやっていた伊豆半島の仁科の佐波神社に残る棟札に地震の記録が書かれた興味深い記事が載っているということで早速調べてみた。
歴史学者磯田道史氏が書いている歴史コラムだ。奇しくも地震の記事である。曰く、
※秋山富南(あきやまふなん、1723~1808年、字は章、通称文蔵)が著した「豆州志稿」は、その他の多くの地誌が村落ごとに記述されるのに対し、沿革・郡郷・租税・原野・川渓・橋梁・物産・神祠・仏刹・古墳・流寓・人物といった項目別になっているが、この富南の「豆州志稿」は江戸時代に印刷・刊行されることはなかった。1888年(明治21)に伊豆長岡の国学者はぎわらしょうへい萩原正平(はぎわらしょうへい、1839~1891年)がこの増補訂正・刊行を企て、正平の死後は嗣子まさお正夫が父の遺志を引き継いで1892年から1895年にかけて『増訂豆州志稿』として印刷・版行した。
婆様がメール打ち込みの練習になるからといって、塾友のYM女史にご機嫌伺いのメールを出したという。その返信に曰く、
早速 BS BHK 午後9時からの「大沢たかお 神秘の北極圏~光と闇の旅~」を録画しておき、今朝の隅田川の徘徊から帰宅すると、早速再生してみた。
インターネットで調べると、この放送を紹介する6組の動画があった。
http://www.nhk.or.jp/ocean/arctic/movie/
婆様はYM嬢にお礼のメールを入れたらしい。すぐに返信が届いた。曰く、
本当に空一面のオーロラは素晴らしかったです。/さらに、極寒の世界にもびっくりしました。いろんなことが初めてで、いい体験させてもらいました。すべての出来事に感謝です。
一昨日は宝塚にいるKS氏から、昨日は篠山の姪から携帯にメールが入った。
今朝のウェブニュースより
昨日のブログと同じく偶方陣のうちでも、n方陣のnが「4の倍数+2」型の偶方陣のもう一つの作り方について説明する。
このn方陣は先ず、昨日までに説明した「偶方陣の作り方1、2、3」にしたがって、「n-2」型の方陣を作り、これに外周を追加して作ることができる。
 (1)まず、4の倍数型の偶方陣を作る。
(1)まず、4の倍数型の偶方陣を作る。
※左図では、「偶方陣の作り方1」によって、四方陣、八方陣を作っている。
(2)次に、各マス目の数字に、外周のマス目の数の半分を加える。
※左図では、四方陣(4×4)では、外周6×6のマス目20マスの半分10を加え、「方陣4×4」を作り、
八方陣(8×8)では、外周10×10のマス目36マスの半分18を加え、「方陣8×8」を作る。
次に外周を作成する。
(3)右上隅から左へ2マスあけて、1、2、……と順に左端までいれる。
※六方陣では左端は4、十方陣では左端は8となる。
(4)右上隅に次の数を入れ、順次下へ数を入れる。一番下の2つのマス目は残して置く。
※六方陣では5~8まで数を、十方陣では9~16までの数を入れる。
(5)一番上の空欄と右下隅マス目の1つ上のマス目に次の数を入れる。
※六方陣では上の空欄に9、右下隅の上のマス目に10を入れ、
十方陣では上の空欄に17、右下隅の上のマス目に18を入れる。
(6)足して n×n+1 になるように、反対側に数を入れる。最下段の反対は最上段であるが、右下隅の反対側は左上隅であり、左下隅の反対は右上隅である。
※六方陣では 6×6+1=37 であるから、たして37になるよう反対側に数を入れ、
十方陣では 10×10+1=101 であるから、たして101になるよう反対側に数を入れる。
(7)右上隅の3マスと、左へ2マスあけて、次の2マスずつを反対側の数字と入れ替える。
※六方陣では最上段の9、1、2と最下段の28、36、35を入れ替える。
※十方陣では最上段の17、1、2、2マスあけて5、6を、最下段の84、100、99,2マスあけて96、95と入れ替える。
(8)右上隅の1つ下と右下隅の1つ上の数字を反対側(左上隅の1つ下と左下隅の1つ上)の数字と入れ替える。
※六方陣では6と31、および10と27を入れ替え、十方陣では10と91、および18と83を入れ替える。
(9)右端列のほかのマス目は、2マスあけて次の2マスずつを反対の数字と入れ替える。
※六方陣では該当するマス目がないのでそのまま、十方陣では13と88、および14と87を入れ替える。
(10)求めた外周(外周作成図2)と、内側部分の方陣を1つにまとめて、出来上がり。
※六方陣では「外周作成図2」の内側に「方陣4×4」を入れて出来上がり、
十方陣では「外周作成図2」の内側に「方陣8×8」を入れて出来上がる。
このn方陣は先ず、昨日までに説明した「偶方陣の作り方1、2、3」にしたがって、「n-2」型の方陣を作り、これに外周を追加して作ることができる。
※左図では、「偶方陣の作り方1」によって、四方陣、八方陣を作っている。
(2)次に、各マス目の数字に、外周のマス目の数の半分を加える。
※左図では、四方陣(4×4)では、外周6×6のマス目20マスの半分10を加え、「方陣4×4」を作り、
八方陣(8×8)では、外周10×10のマス目36マスの半分18を加え、「方陣8×8」を作る。
次に外周を作成する。
(3)右上隅から左へ2マスあけて、1、2、……と順に左端までいれる。
※六方陣では左端は4、十方陣では左端は8となる。
(4)右上隅に次の数を入れ、順次下へ数を入れる。一番下の2つのマス目は残して置く。
※六方陣では5~8まで数を、十方陣では9~16までの数を入れる。
(5)一番上の空欄と右下隅マス目の1つ上のマス目に次の数を入れる。
※六方陣では上の空欄に9、右下隅の上のマス目に10を入れ、
十方陣では上の空欄に17、右下隅の上のマス目に18を入れる。
(6)足して n×n+1 になるように、反対側に数を入れる。最下段の反対は最上段であるが、右下隅の反対側は左上隅であり、左下隅の反対は右上隅である。
※六方陣では 6×6+1=37 であるから、たして37になるよう反対側に数を入れ、
十方陣では 10×10+1=101 であるから、たして101になるよう反対側に数を入れる。
(7)右上隅の3マスと、左へ2マスあけて、次の2マスずつを反対側の数字と入れ替える。
※六方陣では最上段の9、1、2と最下段の28、36、35を入れ替える。
※十方陣では最上段の17、1、2、2マスあけて5、6を、最下段の84、100、99,2マスあけて96、95と入れ替える。
(8)右上隅の1つ下と右下隅の1つ上の数字を反対側(左上隅の1つ下と左下隅の1つ上)の数字と入れ替える。
※六方陣では6と31、および10と27を入れ替え、十方陣では10と91、および18と83を入れ替える。
(9)右端列のほかのマス目は、2マスあけて次の2マスずつを反対の数字と入れ替える。
※六方陣では該当するマス目がないのでそのまま、十方陣では13と88、および14と87を入れ替える。
(10)求めた外周(外周作成図2)と、内側部分の方陣を1つにまとめて、出来上がり。
※六方陣では「外周作成図2」の内側に「方陣4×4」を入れて出来上がり、
十方陣では「外周作成図2」の内側に「方陣8×8」を入れて出来上がる。
左図に示すように、次の方法でn方陣(nは4の倍数)の準備図1と2を作成する。
 (1) 1行目の左端に1を入れ、次の数を順次2、3、……、nと右へ入れてゆく。
(1) 1行目の左端に1を入れ、次の数を順次2、3、……、nと右へ入れてゆく。
(2) 2行目は、1行目の逆順に数を入れて行く。
(3) 何行目かによって、正順か逆順かが、決まる。
正逆逆正正逆逆正正逆逆正正 ・・・ の順になる。
次に、補助図2を作成する。
(1) 準備図1の行と列を入れ替え、補助図を作る。
(2) 補助図のマス目の数から1を引き、n(魔方陣の大きさ)を掛けた数字に入れ替えたものを準備図2とする。(左図)
最後に、準備図1と準備図2て、同じ位置にある数字をたして、完成図とする。
 左の図は、同じ方法で作った八方陣である。
左の図は、同じ方法で作った八方陣である。
(2) 2行目は、1行目の逆順に数を入れて行く。
(3) 何行目かによって、正順か逆順かが、決まる。
正逆逆正正逆逆正正逆逆正正 ・・・ の順になる。
次に、補助図2を作成する。
(1) 準備図1の行と列を入れ替え、補助図を作る。
(2) 補助図のマス目の数から1を引き、n(魔方陣の大きさ)を掛けた数字に入れ替えたものを準備図2とする。(左図)
最後に、準備図1と準備図2て、同じ位置にある数字をたして、完成図とする。
明らかに二方陣は作ることは出来ない。今日は四方陣・八方陣・十二方陣のように、4の倍数方陣の作り方について説明しよう。
 左図のように、
左図のように、
(1) 中心点(●)を共有する4つのマス目を網掛けにして、これを元に市松模様をつくり、左上から、順番に数字を入れて行く。(準備図)
(2) 網目のないマス目の数字はそのままにして、網目の付いたマス目の数字を、中心点●に対して対称の位置に移し替え(数字を交換すれ)ば出来上がり。(完成図1)
※四方陣では網目は対角線に並ぶマス目についているから、これらの数字、1と16、6と11、4と13、7と10を交換すればよい。
(2') 網目の付いたマス目の数字はそのままにして、編み目のないマス目の数字を、中心点●に対して対称の位置に移し替え(数字を交換して)も出来上がる。(完成図2)
※図の八方陣の完成図は、上の(2')を用いて作成したものである。
以上の方法は、次のように考えても良い。
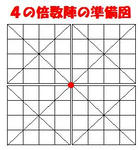 左の図にのように、4の倍数方陣を四方陣のブロックに分けて(八方陣だと4ブロック、十二方陣だと9ブロック)、各ブロックごとに四隅を結ぶ対角線(×印になる)を引く。
左の図にのように、4の倍数方陣を四方陣のブロックに分けて(八方陣だと4ブロック、十二方陣だと9ブロック)、各ブロックごとに四隅を結ぶ対角線(×印になる)を引く。
(1) ブロックに関係なく、左上から順番に1行目・2行目・… と数字(四方陣だと1~16、八方陣だと1~64、十二方陣だと1~144)を入れて行く。
(2)記号の/ 又は \ の上にある数字は中心点●に対し対称の位置に移せば、出来上がり。
(2')記号の/ 又は \ の上にある数字はそのままにして、記号/ 又は \ のない所にある数字を中心点●に対して対称の位置に移動しても出来上がる。
(1) 中心点(●)を共有する4つのマス目を網掛けにして、これを元に市松模様をつくり、左上から、順番に数字を入れて行く。(準備図)
(2) 網目のないマス目の数字はそのままにして、網目の付いたマス目の数字を、中心点●に対して対称の位置に移し替え(数字を交換すれ)ば出来上がり。(完成図1)
※四方陣では網目は対角線に並ぶマス目についているから、これらの数字、1と16、6と11、4と13、7と10を交換すればよい。
(2') 網目の付いたマス目の数字はそのままにして、編み目のないマス目の数字を、中心点●に対して対称の位置に移し替え(数字を交換して)も出来上がる。(完成図2)
※図の八方陣の完成図は、上の(2')を用いて作成したものである。
以上の方法は、次のように考えても良い。
(1) ブロックに関係なく、左上から順番に1行目・2行目・… と数字(四方陣だと1~16、八方陣だと1~64、十二方陣だと1~144)を入れて行く。
(2)記号の/ 又は \ の上にある数字は中心点●に対し対称の位置に移せば、出来上がり。
(2')記号の/ 又は \ の上にある数字はそのままにして、記号/ 又は \ のない所にある数字を中心点●に対して対称の位置に移動しても出来上がる。
プロフィール
ハンドルネーム:
目高 拙痴无
年齢:
93
誕生日:
1932/02/04
自己紹介:
くたばりかけの糞爺々です。よろしく。メールも頼むね。
sechin@nethome.ne.jp です。
sechin@nethome.ne.jp です。
カレンダー
| 12 | 2026/01 | 02 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
最新コメント
[enken 02/23]
[中村東樹 02/04]
[m、m 02/04]
[爺の姪 01/13]
[レンマ学(メタ数学) 01/02]
[m.m 10/12]
[爺の姪 10/01]
[あは♡ 09/20]
[Mr.サタン 09/20]
[Mr.サタン 09/20]
最新トラックバック
ブログ内検索
カウンター
