瘋癲爺 拙痴无の戯言・放言・歯軋り
東山・西川・南野・北原の4家族からそれぞれ、父親・母親・息子・娘の4人が集まって計16人で麻雀大会を開くことになった。テーブルを4卓準備して同時にゲームを進めたいのであるが、組み合わせに次の条件を付けることにした。
条件:どの卓にも東山・西川・南野・北原の家族の誰かが居り、しかも、父親・母親・息子・娘が1人ずつ参加していること。
 この条件を満たす組み合わせは左の1図の通りで、同じテーブルに着くのは、縦の列の4人でも横の行の4人でも良いわけである。すなわち、4次オイラー方陣になっている。オイラー方陣のいわれは、18世紀の数学者Eulerが「士官36人の問題」を出したことに拠ることは、先日説明した通りである。
この条件を満たす組み合わせは左の1図の通りで、同じテーブルに着くのは、縦の列の4人でも横の行の4人でも良いわけである。すなわち、4次オイラー方陣になっている。オイラー方陣のいわれは、18世紀の数学者Eulerが「士官36人の問題」を出したことに拠ることは、先日説明した通りである。
1図の組み合わせで、各家庭だけに目を向ければ、2図が得られ、どの行、どの列にも東山(1)、西川(2)、南野(3)、北原(4)が含まれている。同じように父、母、息子、娘だけに注目空けば、3図が得られ、やはり各行、各列に父(1)、母(2)、息子(3)、娘(4)が含まれている。
どの行、どの列にも異なるものが1つずつ含まれている組み合わせを「ラテン方陣」という。ラテン方陣の名はEulerによるもので、記号としてラテン文字(ローマ字)を用いたことによるといわれている。
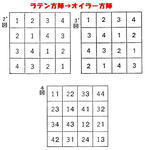 左図のように、2図、3図のラテン方陣を数字で表わすことにすると、2’図、3’図のように見易くなる。そして、オイラー方陣の表わし方も4図のようになり、1~4の数を使った2桁の組み合わせ16個が洩れなく1個ずつ勢ぞろいするのである。
左図のように、2図、3図のラテン方陣を数字で表わすことにすると、2’図、3’図のように見易くなる。そして、オイラー方陣の表わし方も4図のようになり、1~4の数を使った2桁の組み合わせ16個が洩れなく1個ずつ勢ぞろいするのである。
この表わし方を用いると、n次のオイラー方陣とは「1~nまでの1桁の数字で表わした2つのラテン方陣を重ねたとき、2桁の数字がどれも1回ずつ現われているもの」と定義できるのである。
条件:どの卓にも東山・西川・南野・北原の家族の誰かが居り、しかも、父親・母親・息子・娘が1人ずつ参加していること。
1図の組み合わせで、各家庭だけに目を向ければ、2図が得られ、どの行、どの列にも東山(1)、西川(2)、南野(3)、北原(4)が含まれている。同じように父、母、息子、娘だけに注目空けば、3図が得られ、やはり各行、各列に父(1)、母(2)、息子(3)、娘(4)が含まれている。
どの行、どの列にも異なるものが1つずつ含まれている組み合わせを「ラテン方陣」という。ラテン方陣の名はEulerによるもので、記号としてラテン文字(ローマ字)を用いたことによるといわれている。
この表わし方を用いると、n次のオイラー方陣とは「1~nまでの1桁の数字で表わした2つのラテン方陣を重ねたとき、2桁の数字がどれも1回ずつ現われているもの」と定義できるのである。
この記事にコメントする
プロフィール
ハンドルネーム:
目高 拙痴无
年齢:
93
誕生日:
1932/02/04
自己紹介:
くたばりかけの糞爺々です。よろしく。メールも頼むね。
sechin@nethome.ne.jp です。
sechin@nethome.ne.jp です。
カレンダー
| 04 | 2025/05 | 06 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
最新コメント
[enken 02/23]
[中村東樹 02/04]
[m、m 02/04]
[爺の姪 01/13]
[レンマ学(メタ数学) 01/02]
[m.m 10/12]
[爺の姪 10/01]
[あは♡ 09/20]
[Mr.サタン 09/20]
[Mr.サタン 09/20]
最新トラックバック
ブログ内検索
カウンター